Extra questions for Similar triangles

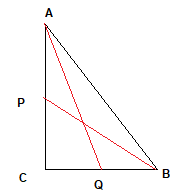
In$\Delta ACQ $
By pythagorus theorem
$AQ^2 = AC^2 + QC^2$
Now $QC = \frac {BC}{2}$

$AQ^2 = AC^2 + (\frac {BC}{2})^2$

$AQ^2 = AC^2 + \frac {BC^2}{4}$
or
$4AQ^2 = 4AC^2 + BC^2$ --(1)
Hence (i) proved

Now In$\Delta BPC$
$BP^2 = BC^2 + PC^2$
Now
$PC= \frac {AC}{2}$
$BP^2 = BC^2 + (\frac {AC}{2})^2$
$BP^2 = BC^2 + \frac {AC^2}{4} $
$4BP^2 = 4BC^2 + AC^2$ --(2)
Hence (ii) proved

Adding (1) and (2)
$4(AQ^2 + BP^2)= 4AC� +BC^2 + AC^2 +4BC^2$
$ 4(AQ^2 + BP^2) = 5(AC^2 + BC^2)$
Now in $\Delta ABC$
$AC^2 + BC^2 = AB^2$

Hence
$4(AQ^2 + BP^2) = 5(AB^2)$

We will need to some construction to apply pythagorus theorem and get the prove then
a. Draw AM perpendicular to side BC
b. Draw BN perpendicular to side AC
c. Draw CK perpendicular to side AB



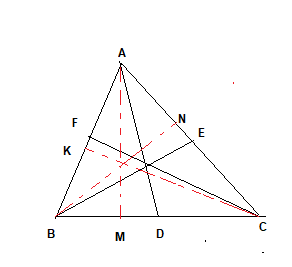
Now it is given that
$BD=DC= \frac {BC}{2}$
$FB=FA= \frac {AB}{2}$
$AE=EC= \frac {AC}{2}$

Now in $\Delta ABM$ and $\Delta AMC$
$AB^2 = AM^2 + BM^2$
$AC^2 = AM^2 + CM^2$
Now BM= BD- MD= DC-MD
and CM= DC + MD
Substituting those values and add equations
$AB^2+ AC^2= 2AM^2 + (DC-MD)^2 + (DC + MD)^2 $
$AB^2+ AC^2= 2AM^2 + DC^2 + MD^2 -2 DC .MD + DC^2 + MD^2 +2 DC .MD$
$AB^2+ AC^2= 2AM^2+ 2DC^2 + 2 MD^2$
$AB^2+ AC^2=2( AM^2 + MD^2 ) + 2 (\frac {BC^2}{4}$
Now from pythagorus theorem in triangle AMD
$AM^2 + MD^2= AD^2$
So,
$AB^2+ AC^2=2 AD^2 + \frac {BC^2}{2}$
Similary we can prove the same equation for the triangles $\Delta BKC$ and $\Delta AKC$
$AB^2+ BC^2=2 AE^2 + \frac {AC^2}{2}$
Similarly for the triangle $\Delta ABN$ and $\Delta BNC$

$AC^2+ BC^2=2 AF^2 + \frac {AB^2}{2}$
Adding three equation,we get
$3 (AB^2 + BC^2 + CA^2) = 4(AD^2 + BE^2 + CF^2)$

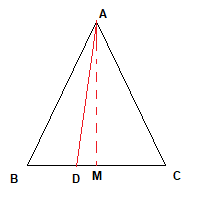
Let draw a perpendicular to line AM to BC

Now we know that Perpendicular bisect the line in equilateral triangle.So
BM= MC

Now in $\Delta ABM$
$AB^2 = BM^2 + AM^2$
$AB^2 = \frac {BC^2}{4} + AM^2$ -(1)
Now in $\Delta AMD$
$AD^2 = AM^2 + MD^2$
Now $MD = BM - BD = \frac {BC}{2} - \frac {BC}{3}= \frac {BC}{6}$
So
$AD^2 =AM^2 + \frac {BC^2}{36}$ --(2)
Subtracting (1) and (2)
$AB^2 - AD^2 = \frac {BC^2}{4} - \frac {BC^2}{36}$
$AB^2 - AD^2=\frac {2BC^2}{9}$
$9AB^2 - 9 AD^2 = 2BC^2$
Now BC=AB
$9AD^2 = 7AB^2$

The Figure is shown below


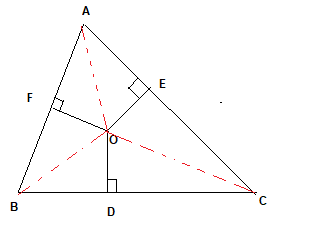
Join the points O and A, O and B, O and C

Now in $\Delta OAE$
$OA^2 = OE^2 + AE^2$ -(1)

Now in $\Delta ODC$
$OC^2 = CD^2 + OD^2$ -(2)
Now in $\Delta OBF$
$OB^2 =OF^2 + BF^2$ -(3)
Adding 1,2,3
$OA^2 + OB^2 + OC^2 - OD^2 - OE^2 - OF^2=AE^2 + CD^2 + BF^2$ -(A)

Now in $\Delta OEC$
$OC^2 = OE^2 +CE^2$ -(4)
Now in $\Delta OBD$
$OB^2 = OD^2 + BD^2$ --(5)
Now in $\Delta OAF$
$OA^2 = Af*2 + OF^2$ --(6)
Adding 4,5,6
$OA^2 + OB^2 + OC^2 - OD^2 - OE^2 - OF^2=AF^2 + BD^2 + CE^2$ -(B)
Hence (a) is proved
From equation (A) and (B)
$AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2$
Hence (b) is proved

In $ \Delta ADC$ and $\Delta BAC$
$ \angle ADC = \angle BAC$
$\angle ACD = \angle BCA$ (Common angle)
Therefore By AA similarity criterion
$ \Delta ADC \sim \Delta BAC $
We know that corresponding sides of similar triangles are in proportion.
So
$ \frac {CA}{CB} ={CD}{CA} $
$CA^2= CB.CD$

Diagram is shown as below

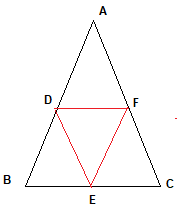
In $ \Delta ADF$ and $\Delta ABC$
$\frac {AD}{AB} = \frac {AF}{FC} = \frac {1}{2}$ ( As D and F are midpoints)
By converse of Basic proportionality theorem
$\Delta ADF \sim \Delta ABC$
and $ \frac {DF}{BC } = \frac {1}{2}$ -(1)

In $ \Delta DBE$ and $\Delta ABC$
$\frac {DB}{AB} = \frac {BE}{BC} = \frac {1}{2}$ ( As D and E are midpoints)
By converse of Basic proportionality theorem
$\Delta DBE \sim \Delta ABC$
and $ \frac {DE}{AC} = \frac {1}{2}$ -(2)

In $ \Delta FCE$ and $\Delta ACB$
$\frac {FC}{AC} = \frac {CE}{CB} = \frac {1}{2}$ ( As E and F are midpoints)
By converse of Basic proportionality theorem
$\Delta FCE$ \sim \Delta ACB$
and $ \frac {EF}{AB} = \frac {1}{2}$ -(3)
From (1) ,(2) and (3)
$\frac {DF}{BC }=\frac {DE}{AC}=\frac {EF}{AB}=\frac {1}{2}$
By SSS criterio
$\Delta DEF \sim \Delta CAB $
Now Area of the similar triangle is given by
$ \frac {area \Delta DEF}{ area \Delta ABC} = \frac {DF^2}{BC^2} = \frac {1}{4}$

It is given that ABC is an isosceles triangle.
Hence AB = AC
$ \angle ABC = \angle ACB$
$ \angle ABD = \angle FCE$ -(1)
Now In $\Delta ABD$ and $ \Delta ECF$
$\angle ADB = \angle EFC$ (Each 90°)
From (1)
$ \angle ABD = \angle FCE$
By using AA similarity criterion
Therefore
$\Delta ABD \sim \Delta ECF$

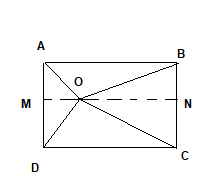
Draw a line MN passing through O and parallel to AB and CD
Now ABCD is a rectangle, then ABNM and MNCD are all rectangles

Now in $\Delta MOD$
$OD^2 = OM^2 + MD^2$
In $ \Delta OBN$
$OB^2 = BN^2 + ON^2$
Adding these
$OB^2 + OD^2=OM^2 + MD^2 + BN^2 + ON^2$
Now BN= AM and MD=NC
$OB^2 + OD^2=(OM^2 + AM^2) + (ON^2 + NC^2)$ -(1)
In triangle AOM
$OA^2 = AM^2 + OM^2$ -(2)
In Triangle ONC
$OC^2 = ON^2 + NC^2$ -(3)
From (1) ,(2) and (3)
$OB^2 + OD^2= OA^2 + OC^2$

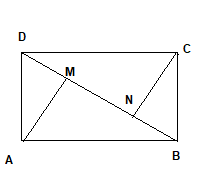
In $\Delta ADM$
$AD^2 = DM^2 + AM^2$ -(1)
In $\Delta DNC$
$CD^2 = DN^2 + CN^2$ -(2)
Adding (1) and (2)
$AD^2 + CD^2=DM^2 + AM^2 + DN^2 + CN^2$ -(A)

In $\Delta AMB$
$AB^2 = AM^2 + BM^2$ -(3)
In $\Delta CNB$
$ BC^2 = BN^2 + CN^2$ -(4)
Adding (3) and (4)
$AB^2 + BC^2 =AM^2 + BM^2 + BN^2 + CN^2$ -(B)
Now AD= BC and AB = CD$ ,putting in equation (B)
$AD^2 + CD^2=AM^2 + BM^2 + BN^2 + CN^2$ --(C)
Subtracting (A) and (C)
$BM^2 + BN^2 = DM^2 + DN^2$

(a) False
(b) True
(c) Here $13^2=12^2 + 5^2$ hence True
(d) True , as the corresponding two sides and the perimeters are three, their third sides will also be three times
(e) False as the Areas of these triangles are in the ratio 25: 121

(14) Let the corresponding side of the larger triangle be x cm. Then, we have 9/x = 3/5, which gives x = 15 cm. So, option (b) is correct
(15) Let angles A and B be x and y degrees, respectively. Then, we have in AOB
$\frac {x}{2} + \frac {y}{2} + 120 =180$
or x+ y=120
Now in Triangle ABC
x + y + C = 180
Therefore C=60 degrees
Hence option(b) is correct
(16) (b)
(17) The ratio of their corresponding sides is the same as the ratio of their perimeters, which is 5:8. Hence, the length of the corresponding side of the larger triangle is (8/5)*4 = 6.4 cm.
Hence (b) is correct
(18) (d) is correct answer as they are similar but not congruent as sides are not equal