Acceleration in a curvilinear motion

The motion of an object moving in a curved path is called curvilinear motion. It can be both two dimension or three -dimension. We will be discussing Acceleration in a curvilinear motion in this post

Example: A stone thrown into the air at an angle.

It is more complex than rectilinear motion

We know for Rectilinear motion (a particle moving in x -direction )

Velocity is given by

$v=\frac{dx}{dt}$

Acceleration is given by

$a=\frac{dv}{dt}$

Now lets discuss this for Curvilinear motion in Three dimension 

Position of particle moving in Three dimension  will be given by

$\mathbf{r}=\left (x \right )\mathbf{i}+\left (y\right )\mathbf{j}+\left ( z \right )\mathbf{k}$

Velocity will be given as

$\mathbf{v}=\left (\frac {dx}{dt} \right )\mathbf{i}+\left (\frac {dy}{dt}\right )\mathbf{j}+\left ( \frac {dz}{dt} \right )\mathbf{k}$

The components of the Velocity along X,Y ,Z are
$v_{x}=\frac{dx}{dt}$
$v_{y}=\frac{dy}{dt}$
$v_{z}=\frac{dz}{dt}$

Magnitude of Velocity

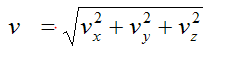
Now Acceleration in a curvilinear motion is given by
$\mathbf{a}=\left ( \frac {dv_{x}}{dt} \right )\mathbf{i}+\left ( \frac {dv_{y}}{dt} \right )\mathbf{j}+\left ( \frac {dv_{z}}{dt} \right )\mathbf{k}$
The components of the acceleration along X,Y ,Z are
$a_{x}=\frac{dv_{x}}{dt}$
$a_{y}=\frac{dv_{y}}{dt}$
$a_{z}=\frac{dv_{z}}{dt}$

Magnitude of acceleration

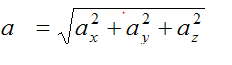
The direction of the velocity is always tangent to the curve. For acceleration,The acceleration vector has the same direction as instantaneous change in velocity. Since the direction of the velocity changes in the direction in which the curve bends ,the acceleration is always pointing towards concavity of the curve

we can write this for two dimensional motion also.It is also called Plane curvilinear motion

Position of particle moving in Two dimension  will be given by

$\mathbf{r}=\left (x \right )\mathbf{i}+\left (y\right )\mathbf{j}$

Velocity will be given as

$\mathbf{v}=\left (\frac {dx}{dt} \right )\mathbf{i}+\left (\frac {dy}{dt}\right )\mathbf{j}$

The components of the Velocity along X,Y  are
$v_{x}=\frac{dx}{dt}$
$v_{y}=\frac{dy}{dt}$

Magnitude of Velocity

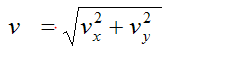
Now Acceleration in a curvilinear motion is given by
$\mathbf{a}=\left ( \frac {dv_{x}}{dt} \right )\mathbf{i}+\left ( \frac {dv_{y}}{dt} \right )\mathbf{j}$
The components of the acceleration along X,Y are
$a_{x}=\frac{dv_{x}}{dt}$
$a_{y}=\frac{dv_{y}}{dt}$

Magnitude of acceleration

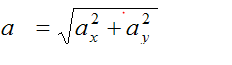
Example

A body is projected horizontally from a point above the ground.The motion of body is defined as
x=2t
y=2t²
where x and y are horizontal and vertical displacement respectivley at time t.Which one of the following is true
a. The trajectory of the body is a parabola
b. The trajectory of the body is a straight line
c. the velocity vector at point t is 2i+4tj
d. the acceleration vector at time t is 4j
Solution

Given
x=2t
y=2t²
Eliminating t we get
y=x²/2
So it is parabola
V_x=dx/dt=2
v_y=dy/dt=4t
So velocity at any time t is given by
v=2i+4tj
Now similary
a_x=dV_x/dt=0
a_y=dV_y/dt=4
So acceleration vector is a=4j

The acceleration in curvilinear motion can also be expressed in terms of two components

a) The tangential component $a_{T}$ which is called as tangential acceleration. It is expressed as change in magnitude of the velocity

b) The normal component $a_{N}$ which is called as normal or centripetal acceleartion. This is expressed as the change in direction of the velocity
$a_{T}=\frac{dv}{dt}$
$a_{N}=\frac{v^2}{R}$
Where R is the radius of curvature of the path

Related Articles

Acceleration formula Explained with Examples

Circular Motion Physics : Detailed explanation