

|
Graph of polynomial |
Number of Zeros |
|
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
a. it cuts the x-axis at two points ,so 2 zeroes
b. it cuts the x-axis at four points ,so 4 zeroes
c. Since it does not cut the axis, so 0 zeroes
d. it cuts the x-axis at 1 points ,so 1 zero’s
e. it cuts the x-axis at 1 points ,so 1 zero’s
f. Since it does not cut the axis, so 0 zeroes
g. Since it does not cut the axis, so 0 zeroes
h. it cuts the x-axis at two points ,so 2 zeroes
|
Graph of polynomial |
Type of polynomial |
|
|
Linear polynomial |
|
|
Quadratic polynomial |
|
|
Cubic polynomial |
|
|
Constant polynomial |
|
|
|
|
|
|
|
|
|
|
|
a. Quadratic as parabola
b. Three zeroes,So cubic polynomial
c. Constant value polynomial
d. Linear polynomial
e. One zeroes but not straight line. So no appropriate match found
f. Quadratic as parabola
g. Quadratic as parabola
e. Cubic as has three zeroes ,two of them same
Answer is ( c)
Let P(x) =x4+x3-2x2+x+1
Remainder when divide by x-1
P(1) = 1+ 1-2+1+1=2
Answer is (d)
a3 + b3= (a+b) (a2+b2-ab)=(a+b) {(a+b)2 -3ab}
Now a+b=-(-11)/1=11
ab=30
So a3+b3=11( 121 -90)=341
S(2)=4p+0+2=0 => p=-1/2
P(x) =(x-11)(x-2)
Dividing p(x) by q(x) ,we get the remainder
(2k-9)x -(8-k)k +10
Comparing this with (x+a)
We get
K=5 and a=-5
(a)
Given that, the zeroes of the quadratic polynomial ax2 + bx + c , c ≠ 0 are equal
Value of discriminant (D) has to be zero
b2– 4ac = 0
b2 = 4ac
Since L.H.S. (b2) can never be negative
R.H.S. also can never be negative.
a and c must have same sign
$p(x)=6x^2 - 7x -3$
$p(x) = 6x^2 -9x + 2x -3 = 3x(2x -3) + 1(2x-3)=(3x+1)(2x-3)
So roots are (3/2) , (-1/3)
Hence option(a) is correct
">
$p(x)=x^2 + 7x +10$
$p(x) = x^2 + 5x +2x +10 = x(x +5) + 2(x+5)=(x+2)(x+5)
So roots are (-2) , (-5)
Hence option(d) is correct
a.(x+6)(x+3)
b.(3x-1)(x-1)(x+1)
c.(x-1)(x-10)(x-12)
d. (2x+1)(4x2-2x+1)
a. r(x)=x3-x2 +4x-5 w(x)=14
b. r(x)=x2-x w(x) =x+4
If $\alpha$ and $\beta$ are the zeroes of the polynomials
$x^2 - (\alpha + \beta) + \alpha \beta$
Here $\alpha + \beta =5 + \sqrt {2} + 5 - \sqrt {2} =10$
$\alpha \beta =(5 + \sqrt {2})(5 - \sqrt {2}) = 25 -4 =21$
Therefore quadratic Polynomial is
$x^2 - 10x + 21$
Here $a + b= -\frac {4}{k}$
$ab=\frac {4}{k}$
Now $(a+b )^2- 2ab= 24$
$(-\frac {4}{k})^2 -2 \frac {4}{k}=24$
$16-8k=24k^2$ or $3K^2 +k-2=0$
$k=-1$ or $k=\frac {2}{3}$
Let a be one of zero, then 1/a be the another zero
Now $a \times \frac {1}{a} =\frac {p}{3}$
or p=3
Here $ p + q=\frac {3}{k}$
$pq=\frac {2k}{k}$
Now
$p+q=pq$
$\frac {3}{k} = 2$
$k= \frac {3}{2}$
Here $a + b= - \frac {-6}{1} = 6$ --(1)
$ab= k$ -(3)
Given $3a+2b= 20$ --(2)
Solving (1) and (2)
a=14 and b=-8
Now substituting these values in (3)
k=-112
Since 2 is zero of the quadratic polynomial
$2^2 + 3 \times 2 + k=0$
k=-10
Now $x^2 + 8x + 16$
$= x^2 + 4x + 4x + 16 = x(x+4) + 4(x+ 4) = (x+4)^2$
So zeroes are -4 ,-4
Now if $k_1$ ,$k_2$ are the roots of quadratic polynomials $ax^2 + bx + c$, then relationship between them is given by
$k_1 + k_2 = -\frac {b}{a}$ and $k_1 k_2= \frac {c}{a}$
Now lets verify the relationship in the above polynomial
$-4 + (-4) = -\frac {8}{1}$
$-8=-8$
Also
$(-4) \times (-4) = \frac {16}{1}$
16=16
Here
$a + b= -a$ or $2a + b=0$ -(1)
Also $ab= b$ or $a=1$
Substituting the value of a in (1)
b=-2
Hence a=1 and b=-2
Here $m + n= = \frac {11}{3}$
$mn= \frac {-4}{3}$
Now
$ \frac {m}{n} + \frac {n}{m} = \frac {m^2 + n^2}{mn} = \frac {(m+n)^2 -2mn}{mn} = \frac {-145}{12}$
$4 \sqrt {3} x^2 + 5x - 2 \sqrt {3}$
$= 4 \sqrt {3} x^2 + 8x -3x - 2 \sqrt {3}$
$= 4x (\sqrt {3}x + 2) - \sqrt {3}(\sqrt {3}x + 2)$
$= (4x - \sqrt {3})(\sqrt {3}x + 2)$
Here $ p + q = 5$ -(1)
$pq= k$ -(2)
Given $p-q= 1$ - (3)
From (1) and (3)
p=3, q=2
Substituting these values in (2)
k=6
Here $ a + b=-\frac {-4}{1} =4$
$ab=3$
$a^4 b^3 + a^3 b^4 = a^3b^3(a +b) = 27 \times 4 = 108$
Here
$a + b =p$ and $ab=q$
Now LHS
$= \frac {a^2}{b^2} + \frac {b^2}{a^2}$
$= (\frac {a}{b} + \frac {b}{a})^2 -2$
$= ( \frac {a^2 + b^2}{ab})^2 -2 $
$=(\frac {(a+b)^2 - 2ab}{ab})^2 -2 = (\frac {p^2 -2q}{q})^2 -2$
$=\frac {p^4 +4q^2 -4p^2q}{q^2} -2 = \frac {p^4}{q^2} +4 - 4\frac {p^2}{q} -2$
$= \frac {p^4}{q^2} - 4\frac {p^2}{q} +2$
=RHS
If √3 and -√3 are zeroes of the polynomial, then $(x- \sqrt {3})(x+ \sqrt {3}) = x^2 -3$ should be factor of it.
$x^3 - 4x^2 - 3x + 12= x^2(x-4) -3(x -4) = (x^2 -3)(x-4)$
Clearly the other zero is 4
Here $l+m= \frac {5}{2}$
$lm= \frac {7}{2}$
Now the polynomial whose zeroes are $2l+ 3$ and $2m+ 3$ is given by
$x^2 - (2l+3 + 2m + 3)x +(2l+3)(2m+3)=x^2 -2(l+m)x -6x + 4lm + 6l + 6m +9$
$=x^2 -10x -6x + 14 + 6(l+m) +9$
$=x^2 -16x +14+15+9=x^2 -16x + 38$
Here $pq + qr+ pr=\frac {-5}{6}=- \frac {5}{6}$
$pqr= -\frac {1}{6}$
Now
$\frac {1}{p} + \frac {1}{q} + \frac {1}{r}$
$= \frac {pq+ qr + pr}{pqr} =5$
Given Roots of given polynomial is in AP
let p-q, p, and p+q are the roots of
$f( x) = ax^3 + 3bx^2 + 3cx + d$
Now we know that
$sum \; of \; roots = - \frac {coefficient \; of \; x^2} {coefficient \;of\; x^3}$
$p-q +p + p+q = - \frac {3b}{a}$
or $3p = - \frac {3b}{a}$
or $p = - \frac {b}{a}$ -----------(1)
Also,
$sum \; of \; products \; of \; two roots = \frac {coefficient \; of\; x}{coefficient \; of \; x^3}$
$ (p -q)\times p + p \times (p+q) + (p-q)(p+q)=\frac {3c}{a}$
$3p^2 - q^2 = \frac {3c}{a}$ ------------------(2)
Also,
$products \; of \; all \; roots = -\frac {constant }{coefficient \; of \; x^3}$
$(p-q)\times p \times (p+q) = -\frac {d}{a}$
$p^3 - pq^2 = -\frac {d}{a}$ ----------(3)
Substituting the value of p from (1) in (2), we get the value of q as
$ 3 (-\frac {b}{a})^2 - q^2 = \frac {3c}{a}$
or
$q^2 = 3 \frac {b^2}{a^2} - 3 \frac {c}{a}$ ----------(4)
Now that we have got the values of p and q, substituting these in equation (3)
$(- \frac {b}{a})^3 +\frac {b}{a}( 3 \frac {b^2}{a^2} -3\frac {c}{a}) = -\frac {d}{a}$
$- \frac {b^3}{a^3} + \frac {b}{a}(3 \frac {b^2}{a^2} -3\frac {c}{a} ) = -\frac {d}{a}$
$- \frac {b^3}{a^3} +3 \frac {b^3}{a^3} -3 \frac {bc}{a^2} = -\frac {d}{a}$
$2\frac {b^3}{a^3} -3 \frac {bc}{a^2} = -\frac {d}{a}$
$2b^3 -3abc + a^2d = 0$
If √(3/2) and -√(3/2) are zeroes of the polynomial, then $(x- \sqrt {3/2})(x+ \sqrt {3/2}) = 2x^2 -3$ should be factor of it.
$f(x) = 2x^4 - 2x^3 - 7x^2 + 3x + 6$
Lets use division algorithm to find the other factors
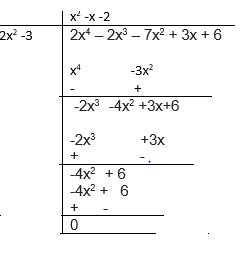
So,
$2x^4 - 2x^3 - 7x^2 + 3x + 6= (2x^2 -3)(x^2 -x -2) = (2x^2 -3)(x^2 -2x + x-2) =(2x^2 -3)(x-2)(x+1)$
So other zeros are x=2 and x=-1
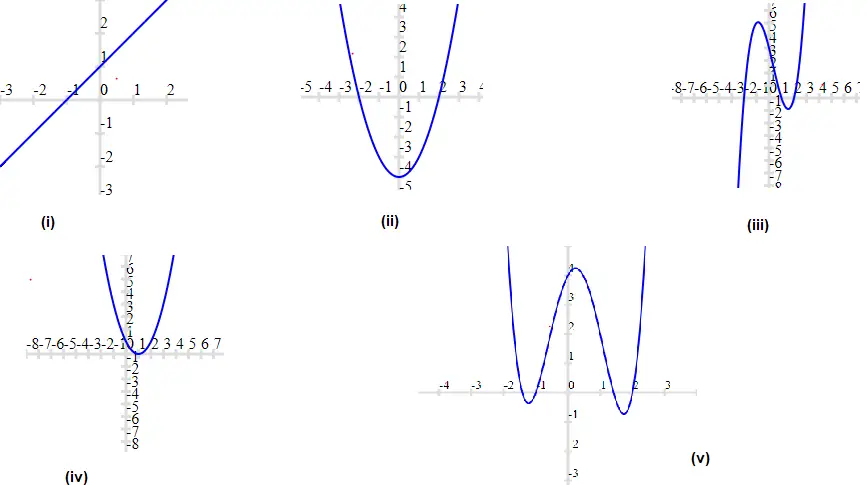
i. 1
ii. 2
iii. 3
iv 1
v. 4
This Class 10 Maths Extra Questions for Polynomials with answers is prepared keeping in mind the latest syllabus of CBSE . This has been designed in a way to improve the academic performance of the students. If you find mistakes , please do provide the feedback on the mail.
