Motion Under Central Forces (part 2)

This article covers topics like Law of conservation of energy, Equation of motion and Form of motion under the effect of central forces.

Law of conservation of energy

From equation 4 we consider
\[f(r) = – \frac{{du(r)}}{{dr}}\]
then this shows that \(f(r)\) is not only a central force but a conservative force. In this condition this equation

also express the law of conservation of energy.
Putting equation 8 in 4 we get
\[m\frac{{{d^2}r}}{{d{t^2}}} – \frac{{r{J^2}}}{{m{r^4}}} = – \frac{{du}}{{dr}}\]
or,
\[m\frac{{{d^2}r}}{{d{t^2}}} = – \frac{{du}}{{dr}} + \frac{{r{J^2}}}{{m{r^4}}}\]
Since we know that
\[\frac{d}{{dr}}\left( {\frac{1}{{{r^2}}}} \right) = – \frac{2}{{{r^3}}}\]
Therefore
\[m\frac{{{d^2}r}}{{d{t^2}}} = – \frac{d}{{dr}}\left( {u + \frac{{{J^2}}}{{2m{r^2}}}} \right)\tag{10}\]
\[m\left( {\frac{{dr}}{{dt}}} \right)\left( {\frac{{{d^2}r}}{{d{t^2}}}} \right) = – \frac{{dr}}{{dt}}\frac{d}

{{dr}}\left( {u + \frac{{{J^2}}}{{2m{r^2}}}} \right)\]
by which
\[\frac{d}{{dt}}\left[ {\frac{1}{2}m{{\left( {\frac{{dr}}{{dt}}} \right)}^2}} \right] = – \frac{d}{{dt}}\left( {u + \frac{{{J^2}}}{{2m{r^2}}}} \right)\]
or,

\[\frac{d}{{dt}}\left[ {\frac{1}{2}m{{\left( {\frac{{dr}}{{dt}}} \right)}^2} + u + \frac{{{J^2}}}{{2m{r^2}}}} \right] = 0\tag{11}\]
or,
\[\left[ {\frac{1}{2}m{{\left( {\frac{{dr}}{{dt}}} \right)}^2} + u + \frac{{{J^2}}}{{2m{r^2}}}} \right] = {\rm{constant}} = E(let)\tag{12}\]
Equation 12 shows the conservation of total energy. In equation 12 term $\frac{1}{2}m{\left( {\frac{{dr}}{{dt}}} \right)^2}$ represents transversal kinetic energy and term \({\frac{{{J^2}}}{{2m{r^2}}}}\) is rotational

kinetic energy and \(u\) is the potential energy.
Here,
\[\frac{{{J^2}}}{{2m{r^2}}} = {\left( {m{r^2}\frac{{d\theta }}{{dt}}} \right)^2}\frac{1}{{2m{r^2}}} = \frac{1}{2}m{r^2}{\left( {\frac{{d\theta }}{{dt}}} \right)^2} = \frac{1}{2}I{\omega ^2}\tag{13}\]

Equation of motion (equation of path of moving particle)

Equation 12 can be written as follows,
\[\frac{{dr}}{{dt}} = {\left[ {\frac{2}{m}\left( {E – u – \frac{{{J^2}}}{{2m{r^2}}}} \right)} \right]^ {{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}}}\]
\[dt = {\left[ {\frac{2}{m}\left( {E – u – \frac{{{J^2}}}{{2m{r^2}}}} \right)} \right]^{ – {\raise0.5ex\hbox {$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}}}dr\tag{14}\]
On integrating left hand side from \(\theta \) to \(t\) and right hand side from \({{r_0}}\) to \({{r}}\) we get
\(\int\limits_0^t {dt} = \int\limits_{{r_0}}^r {{{\left[ {\frac{2}{m}\left( {E – u – \frac{{{J^2}}}{{2m{r^2}}}} \right)} \right]}^{ – {\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}}}dr} \tag{15}\)
We also know that angular momentum
\[J = m{r^2}\left( {\frac{{d\theta }}{{dt}}} \right)\]
\[d\theta = \frac{J}{{m{r^2}}}dt\]
\[\theta = \int\limits_0^t {\frac{J}{{m{r^2}}}dt} \tag{16}\]
Here \({{r}}\) is dependent on \({{t}}\).
Equations 15 and 16 are theoretically used to explain the relation between \({{r}}\) and \({{t}}\) and \(\theta \) and \({{t}}\) if we know the nature of central forces from equation 14. Now if we put \(dt\) in terms of \({{r}}\) in equation 16 and solve it , then its solution shows the progress of motion. In other words we can say that polar co-ordinates \({{r}}\) and \(\theta \) of a particle can be known with respect to time \({{t}}\) otherwise path of moving particle under central forces can be known by eleminating \({{t}}\) from equation 4.
We know that
\[J = m{r^2}\left( {\frac{{d\theta }}{{dt}}} \right)\]
\[\frac{{d\theta }}{{dt}} = \frac{J}{{m{r^2}}}\frac{{d(\theta )}}{{d(\theta )}}\]
Therefore in the form of operator
\[\frac{d}{{dt}} = \frac{J}{{m{r^2}}}\frac{d}{{d\theta }}\]
and
\[\frac{d}{{dt}}\left( {\frac{d}{{dt}}} \right) = \frac{J}{{m{r^2}}}\frac{d}{{d\theta }}\left( {\frac{J}{{m{r^2}}} \frac{d}{{d\theta }}} \right)\]
this implies that
\[\frac{{{d^2}}}{{d{t^2}}} = \frac{{{J^2}}}{{{m^2}{r^4}}}\frac{{{d^2}}}{{d{\theta ^2}}}\tag{17}\]
Now from equation 4
\[m\left[ {\frac{{{d^2}r}}{{d{t^2}}} – r{{\left( {\frac{{d\theta }}{{dt}}} \right)}^2}} \right] = f(r)\]
\[m\left[ {\frac{{{J^2}}}{{{m^2}{r^4}}}\frac{{{d^2}r}}{{d{\theta ^2}}} – r\frac{{{J^2}}}{{{m^2}{r^4}}}} \right] = f(r)\]
\[\frac{{{J^2}}}{{m{r^2}}}\frac{d}{{d\theta }}\left( {\frac{1}{{{r^2}}}\frac{{dr}}{{d\theta }}} \right) – \frac {{{J^2}}}{{m{r^3}}} = f(r)\]
but
\[\frac{1}{{{r^2}}}\frac{{dr}}{{d\theta }} = – \frac{d}{{d\theta }}\left( {\frac{1}{r}} \right)\]
therefore
\[\frac{{{J^2}}}{{m{r^2}}}\left[ {\frac{{{d^2}}}{{d{\theta ^2}}}\left( {\frac{1}{r}} \right) + \left( {\frac{1}{r}} \right)} \right] = – f(r)\tag{18}\]
if \(u = \left( {\frac{1}{r}} \right)\) , then
\[\frac{{{J^2}{u^2}}}{m}\left[ {\frac{{{d^2}u}}{{d{\theta ^2}}} + u} \right] = – F\left( {\frac{1}{u}} \right) \tag{19}\]
This equation is the equation of path of moving particle. This can be solved if nature and magnitude of force is known. If path of the moving particle is known then we can find about the nature of the force.

Form of motion under the effect of central forces

According to equation 10
\[m\frac{{{d^2}r}}{{d{t^2}}} = – \frac{d}{{dr}}\left( {u + \frac{{{J^2}}}{{2m{r^2}}}} \right) = – \frac{{du’}}{{dr}} = f'(r)\]
where,\(u’ = \left( {u + \frac{{{J^2}}}{{2m{r^2}}}} \right)\)
that is
\[f'(r) = – \frac{{du}}{{dr}} – \frac{d}{{dr}}\left( {\frac{{{J^2}}}{{2m{r^2}}}} \right)\]
\[f'(r) = f(r) + \frac{{{J^2}}}{{m{r^3}}}\tag{20}\]
Here, \({\frac{{{J^2}}}{{2m{r^2}}}}\) is potential energy. According to centrifugal forces
\[\frac{{{J^2}}}{{m{r^3}}} = m{\omega ^2}r\]
Now we can write the magnitude of total energy from equation 12
\[E = \frac{1}{2}m{\left( {\frac{{dr}}{{dt}}} \right)^2} + u + \frac{{{J^2}}}{{2m{r^2}}}\]
or,
\[E = \frac{1}{2}m{\left( {\frac{{dr}}{{dt}}} \right)^2} + u’\tag{21}\]
Hence
\[u’ = u + \frac{{{J^2}}}{{2m{r^2}}}\]
Inverse square central forces curves for \(u\) , \(u’\) and \(\frac{{{J^2}}}{{2m{r^2}}}\) are shown below in the figure.

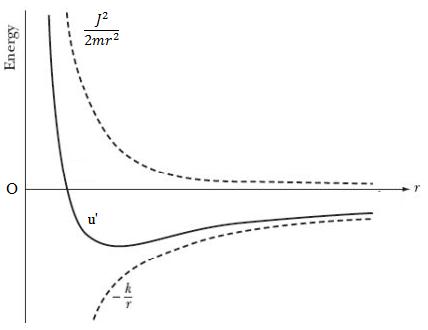
Here magnitude of kinetic energy is \(\frac{1}{2}m{\left( {\frac{{dr}}{{dt}}} \right)^2}\) and is always positive. Also centrifugal energy \(\frac{{{J^2}}}{{2m{r^2}}}\) is positive whereas potential energy \(u\) can be positive as well as negative. \(u’ = u + \frac{{{J^2}}}{{2m{r^2}}}\) that is effective potential energy can be positive or negative.
Positive magnitude of \(u’\) means
\[\left| {\frac{{{J^2}}}{{2m{r^2}}}} \right| > \left| u \right|\]
Negative magnitude of \(u’\) means
\[\left| {\frac{{{J^2}}}{{2m{r^2}}}} \right| < \left| u \right|\]
Therefore the positive and negative values of \(u’\) will depend on the relative magnitude of \(u\) and \(\frac{{{J^2}}}{{2m{r^2}}}\)