Frame of Reference
The motion of different bodies can be conveniently described if we imagine a coordinate system attached to a rigid body and the positions of different bodies in space can be described w.r.t. it, then such a coordinate system is called frame of reference.
For example, we at rest relative to earth along with earth and laboratories build on earth etc., constitute a frame of reference. It is with respect to this Earth’s frame of reference that we observe and measure the changes of positions of other objects. Similar frames of reference can be associated with the objects that may not be at rest relative to us.
Within a frame of reference, we set up a coordinate system which is used to measure the position of an object and choose our origin accordingly. Here we will assume that space is flat, three dimensional and Euclidean.
In general, three coordinate systems are used:
- Rectangular or cartesian
- Spherical or polar
- Cylindrical
In general, for the location of an event in a frame of reference or coordinate system, we require its position and time of occurrence of the event. So, in this case of rectangular or Cartesian coordinate system, four coordinates are required to describe the position that is $(x,y,z,t)$. The reference system employed for this purpose is called a space-time frame of reference.
Rectangular Cartesian coordinate system
In mechanics, you know the motion of material particle/ bodies when you know its position in space at all instants of time.
In this system, three dimensions are represented by three-axis x, y, z perpendicular to each other. Co-ordinates of any point in space are taken as distances from the origin along the three axes and are written as $(x,y,z)$ This coordinate system is generally used when no special symmetry is involved.
Now the ranges for the coordinate parameters are:
$ – \infty \leqslant x \leqslant \infty $
$ – \infty \leqslant y \leqslant \infty $
$ – \infty \leqslant z \leqslant \infty $
There are two independent rectangular coordinate systems possible in space
- Left-handed system
- Right-handed system
These two systems cannot be made to coincide with each other by any means of translation or rotation.
By convention, we choose right-handed coordinate system is preferred over a left-handed system and is shown below in the figure
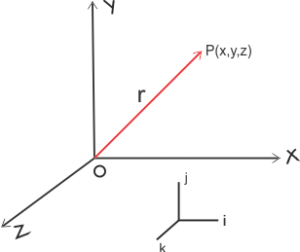
Here the position of the particle $P$ relative to the origin $O$ is given by position vector $r$
$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$
Where $\hat{i}$ , $\hat{j}$ and $\hat{k}$ are unit vectors in directions of $X$, $Y$ and $Z$ axes.
Displacement:-
Consider the figure given below where point $P$ is at point $(x,y,z)$. From the figure, we can clearly see that we are dealing with the right-handed rectangular coordinate system. In vector form displacement of $P$ from $O$ is given by vector $\vec r$ which is
$\vec r = x\hat i+x\hat j+z\hat k$
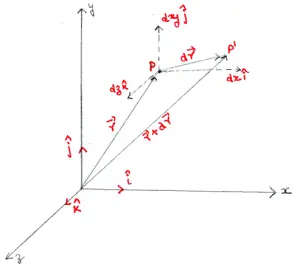
We can write vectorial increment $d\vec r$ in $\vec r$ as
\begin{equation}
d\vec r =d\vec x+d\vec + yd\vec z = dx\hat i +dy\hat j+dz\hat k \label{ref1}
\end{equation}
Sometimes $d\vec r$ is also expressed as $d\vec s$.
Question: Draw a volume element in right-handed coordinate system find the areas of sides that are perpendicular to each other. Also, write these areas in vector form. In the end, find the volume of this volume element.
Velocity and acceleration in the Cartesian coordinate system
Velocity :-
We know that velocity is the rate of change of displacement. So, differentiating the equation \eqref{ref1} we get,
\begin{align}
\vec{v} & = \frac{d}{dt} \vec{r}\notag \\
& = \frac{d}{dt} (r\hat r)\notag \\
& = \frac{dr}{dt}\hat r + r\frac{d\hat r}{dt}\label{ref2}
\end{align}
In the above equation \ref{ref2} velocity contains two parts
1. First part consists of the contribution from the change of $|\vec r| = r$ (magnitude of vector $\vec r$ in the direction of unit vector $\hat r$.
2. Second part is due to change in unit vector $\hat r$.
Also, from the equation \ref(ref1} differentiating with respect to time, we get
\begin{align}
\vec v &=\frac{d\vec x}{dt}+\frac{d\vec y}{dt}+\frac{d\vec z}{dt} \notag \\
&=\dot{\vec x}+\dot{\vec y}+\dot{\vec z}\notag \\
&=\dot{x}\hat i+\dot{y}\hat j+\dot{z}\hat k
\end{align}
The magnitude of $\vec v$ is given by
\begin{equation}
\left | \vec v \right |=\left ( \dot{x}^2 +\dot{y}^2+\dot{z}^2 \right )^{\frac{1}{2}}
\end{equation}
Acceleration:-
Again, accelerationis the rate of change of velocity. differentiating \ref{ref2} with respect to time we get acceleration $\vec a$ as,
\begin{align}
\vec a &=\frac{d\vec v}{dt}=\frac{d \dot{\vec x}}{dt}+\frac{d \dot{\vec y}}{dt}+\frac{d \dot{\vec z}}{dt}\notag \\
&=\ddot{\vec x}+\ddot{\vec y}+\ddot{\vec z}\notag \\
&=\ddot{x}\hat i+\ddot{y}\hat j+\ddot{z}\hat k
\end{align}
The magnitude of $\vec a$ is given by
\begin{equation}
\left | \vec a \right |=\left ( \ddot{x}^2 +\ddot{y}^2+\ddot{z}^2 \right )^{\frac{1}{2}}
\end{equation}

