Welcome to our webpage dedicated to providing Class 11 physics students with sample papers and solutions. On this page, you will find a variety of questions and answers, all prepared according to the CBSE Class 11 physics syllabus. PDF download of this sample paper is also available.
This website offers a sample paper for class 11 physics students that includes a range of question formats based on the CBSE syllabus, such as very short answer questions, MCQs, case study based questions, short answer questions, and long answer questions.
These questions are designed to evaluate students’ understanding of important ideas and terminology, as well as their ability to apply knowledge to real-world circumstances, problem-solving abilities, and capacity to explain and elaborate on physics concepts.
In addition to the sample papers, we also offer detailed study materials for Class 11 physics. Be sure to visit our Class 11 page for more information and resources to help you excel in your studies.
Class 11 physics sample papers with solutions
Maximum Marks: 70 Marks Time Allowed: 3 hours General Instructions
- All questions are compulsory. There are 33 questions in all.
- This question paper has five sections: Section A, Section B, Section C, Section D, and Section E.
- Section A contains 7 very short answer questions and seven MCQs of one mark each and
Section B has two case study-based questions of 4 marks each,
Section C contains nine short answer questions of 2 marks each,
Section D contains five short answer questions of 3 marks each and
Section E contains three long answers five marks each. - There is no overall choice. However internal choice is provided. You have to attempt only one of the choices in such questions.
Sample Paper for class 11 physics full syllabus
Section – A: All questions are compulsory. All questions in this section contain one mark each.
Q 1. The pair of quantities having the same dimensions are
(a) Impulse and Surface Tension
(b) Angular momentum and Work
(c) Work and Torque
(d) Young’s modulus and Energy
Q 2. Percentage errors in the measurement of mass and speed are 2% and 3% respectively. The error in the estimate of kinetic energy obtained by measuring mass and speed will be
(a) 8%
(b) 2%
(c) 12%
(d) 10%
Q 3. A particle moves in a straight line and covers half the distance with a speed of 3 m/s. The other half of the distance is covered in two equal time intervals with speeds of 4.5 m/s and 7.5 m/s, respectively. The average speed of the particle during this motion is
(a) 4.0 m/s
(b) 5.0 m/s
(c) 5.5 m/s
(d) 4.8 m/s
Q 4. Which of the following graphs shows the v-t graph of a ball thrown upwards?
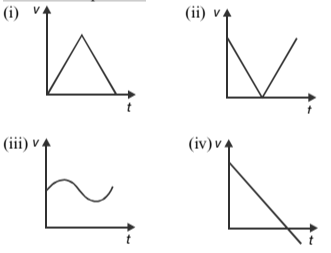
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Q 5. In the following questions, a statement of assertion is followed by a statement of reason. You are required to choose the correct one out of the given five responses and mark it as
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not correct explanation of the assertion.
(c) If assertion is true, but reason is false.
(d) If both assertion and reason are false.
(e) If reason is true but assertion is false.
Assertion: It is difficult to move a cycle along the road with its brakes on.
Reason: Sliding friction is greater than rolling friction.
Q 6. A particle moves along a curve of unknown shape but the magnitude of force $\vec F$ is constant and always acts along the tangent to the curve. Then,
(a)$\vec F$ must be conservative
(b) $\vec F$ may be conservative
(c) $\vec F$ must be non-conservative
(d) $\vec F$ may be non-conservative
Q 7. Two springs P and Q are stretched by applying forces of equal magnitudes at the four ends. If the spring constant of P is 2 times greater than that of Q and the energy stored in P is E, then the energy stored in Q is
(a) $\frac{E}{4}$
(b) $\frac{E}{2}$
(c) $E$
(d) $2E$
Q 8. Can the relative velocity of two bodies be greater than the absolute velocity of either?
Q 9. What would be the numerical value of Young’s modulus for an ideal elastic body?
Q 10. Can a system be heated and its temperature remains constant?
Q 11. Is it possible that the Centre of mass lies where there is no mass? Give one example.
Q 12. Which object will cool faster when kept in the open air, the one at $300^0C$ or the one at $100^C$? Why?
Q 13. A body is moving along a circular path. How much work is done by the centripetal force?
Q 14. What is the minimum possible temperature on the basis of Charle’s Law?
Section -B: Questions 15 and 16 are case study-based questions and are compulsory. Attempt any 4 sub-parts from each question. Each question carries 1 mark.
Q 15. A seesaw is a simple machine that explains the idea of balance and rotational equilibrium. It is made up of a board that is balanced on a pivot point and may rotate back and forth. When two people of equal weight sit at opposite ends of a seesaw, their weights are balanced, and the seesaw maintains rotational equilibrium.
1. The balance in the beam is maintained when
(a) the clockwise moments about the pivot point are equal to the anticlockwise moment about that point.
(b) Weight of two people or the load on opposite ends of the board must be the same.
(c) Weight of two people or the load on opposite ends of the board must be different.
(d) the clockwise moments about the pivot point are not equal to the anticlockwise moment about that point.
2. Assume two people of equal weight sit on opposing sides of a seesaw. We have now cut the distance between the pivot point and the board on the left side in half when compared to the board on the right side. Select the correct statement based on this situation.
(a) moment of force is greater on the left-hand side
(b) moment of force is the same on both the sides
(c) moment of force is more on the right-hand side
(d) moment of force on the left-hand side is double what it is on the right-hand side.
3. We now have a seesaw with two children seated at equal distances from the pivot point. Now the weight of the child on the left-hand side is more than that of the child on the right-hand side. Select the correct statement based on this situation.
(a) Child on right would lift the other child easily.
(b) Child on left would lift the other child easily
(c) Both of them would use the same effort to lift one another
(d) None of the options are correct
4. The moment of the couple is equal to the product of either of the forces and the perpendicular distance, called the arm of the couple, between the line of action. Hence moment of a couple is
(a) dependent on the choice of point of rotation
(b) independent of the perpendicular distance between the forces
(c) independent of the choice of point of rotation.
(d) depends on the perpendicular distance between the forces and the choice of point of rotation.
Q 16. In a refrigerator, the heat energy is transferred from the inside of the refrigerator to the outside, making the inside of the refrigerator cooler. The first law of thermodynamics is the general law of energy conservation that applies to every system that involves energy transfer from or to the surroundings (by heat and work). It states that the energy given to the system is used to improve the system’s internal energy and the remainder is used to work on the environment.
Cooling of the Refrigerator also follows the first law of thermodynamics. Mathematically,
$\Delta Q = \Delta U + \Delta W$ where $\Delta Q$ is the heat supplied to the system, $\Delta W$ is the work done by the system, and $\Delta U$ is the change in internal energy of the system.
$\Delta Q$ and $\Delta W$ depend on the path taken to go from initial to final states, but the combination $\Delta Q – \Delta W$ is path independent.
1. The first law of thermodynamics is concerned with the conservation of
(a) number of molecules
(b) number of moles
(c) energy
(d) temperature
2. Which of the following is not a path function?
(a) $\Delta Q$
(b) $\Delta Q +$\Delta W$
(c) $\Delta W$
(d) $\Delta Q – \Delta W$
3. Which of the following is true in the case of adiabatic expansion
(a) $\Delta U=0$
(b) $\Delta U=negative$
(c) $\Delta U=positive$
(d) $\Delta W=0$
4. The heat given to an ideal gas in isothermal conditions is used to
(a) increase temperature
(b) do external work
(c) increase temperature in doing external work
(d) increase internal energy
SECTION C: All questions are compulsory. In case of internal choices, attempt any one of them. (2 Marks)
Q 17. If force $F$, length $L$, and time $T$ are taken as fundamental units then what would be the dimensions of mass?
OR
The magnitude of force $F$ experienced by a certain object moving with a speed $v$ is given by relation $F=kv$, where $k$ is a constant. Find the dimensions of $k$
Q 18. Prove that the horizontal range is the same when the angle of projection is
(1) greater than $45^0$ by a certain value
(2) less than $45^0$ by the same value
Q 19. State the law of conservation of linear momentum. What is the necessary condition to conserve it?
Q 20. Why does a solid sphere have a smaller moment of inertia than a hollow cylinder of the same mass and radius about an axis passing through its axis of symmetry?
Q 21. What is the gravitational potential energy of a body at height $h$ from the Earth’s surface?
Q 22. A liquid drop breaks into 27 small drops. If the surface tension of the liquid is $S$, then find the energy released.
Q 23. Write two limitations of the first law of Thermodynamics.
Q 24. The maximum acceleration of a simple harmonic oscillator is $a_0$ and the maximum velocity is $v_0$. What is the displacement amplitude?
Q 25. You have a light spring, a meter scale, and a known mass. How will you find the time period of vibration of mass without the use of a clock?
SECTION D: All questions are compulsory. (3 Marks)
Q 26. A capacitor of capacitance $C=(2.0\pm 0.1)\mu F$ is charged to a voltage $V=(20\pm 0.5)V$. Calculate the charge $Q$ with error limits. (relation between these three quantities is $Q=CV$)
Q 27. Define centripetal acceleration. Find the expression for it. Give one example of centripetal force.
Q 28. Two protons are brought towards each other. Will the potential energy of the system decrease or increase? If the proton and electron are brought nearer, then?
Q 29. Two stationary particles of masses $M_1$ and $M_2$ are a distance $d$ apart. A third particle lying on the line joining the particles, experiences no resultant gravitational force. What is the distance of this particle from $M_1$?
Q 30. Calculate the average kinetic energy for one molecule of gas at constant volume.
SECTION E: All questions are compulsory. (5 Marks)
Q 31. Derive three equations of motion using the graphical method. Which physical quantity is obtained?
1. Slope of velocity time graph
2. Area under the velocity time graph.
Q 32. Write Bernoulli’s principle and what are the limitations of Bernoulli’s principle with the help of a labeled diagram derive its formula mathematically give two examples of applications where the Bernoulli principle is applied in daily life.
Q 33. For a traveling harmonic wave
$y(x,t)=2.0\cos2\pi[10t-0.0080x+0.35]$
where $x$, and $y$ are in cm and $t$ in seconds. Calculate the phase difference between the oscillatory motion of two points separated by a distance of
(a) 4 cm
(b) 0.5 m
(c) $\frac{\lambda}{2}$
(d) $\frac{3\lambda}{2}$
Download this Class 11 physics sample paper as pdf
Solutions for this sample paper
- (d)
- (a). It is given in the question that percentage error in mass and velocity = 2% and 3% respectively $K.E.=\frac{1}{2}mv^2$
percentage error in K.E $=(\frac{\Delta m}{m} \times 100)+(2\times\frac{\Delta v}{v}\times 100)$
=2+6=8% - (a) $t_1=\frac{x/2}{3}=\frac{x}{6}$
$x_1=4.5t_2$, $x_2=7.5t_2$
Also, $ x_1 + x_2 = x/2 = (4.5 + 7.5) t_2$
That is, $t_2=\frac{x}{24}$
$t=t_1+t_2=\frac{x}{6}+\frac{2x}{24}=\frac{x}{4}$ or, $v=\frac{x}{t}=4m/s$ - (d) Velocity of a body projected upward under gravity decreases to reach zero when the body reaches the maximum height. After that velocity reverses its direction and then increases.
- When brakes are on, there is no rolling of the wheels and the wheels slide. The sliding friction is greater than the rolling friction. Thus it is difficult to move a cycle along the road with its breaks on. Hence, the correct answer is option (a)
- Here, the force is tangential to the curve, hence the work done depends on path. Therefore, force $\vec F$ must be non-conservative.
Hence, the correct answer is option (c) - Let the spring constant of spring $Q$ is $k$ and that of $P$ is $2 k$. The extensions produced by applying equal forces on them are $x_P$ and $x_Q$, respectively.
Since $F = kx$ (numerically)
$\Rightarrow\qquad x=\frac{F}{k}$
and,
$U=\frac{1}{2}kx^2$
$\Rightarrow\qquad U=\frac{1}{2}(\frac{F}{k})^2=\frac{F^2}{2k}$
$\Rightarrow\qquad U\propto \frac{1}{k}$
Thus,
$\frac{U_q}{U_P}=\frac{k_P}{k_Q}=\frac{2k}{k}=2$
$\Rightarrow\qquad U_Q=2U_P=2E$
Hence, the correct answer is option (d) - Yes, when two bodies move in opposite direction then relative velocity of each is greater than the individual velocities.
- The value of Young’s modulus will be between 0 to 1 for an ideal elestic body.
- If the system does work against the surroundings so that it compensates for the heat supplied, the temperature can remain constant.
- Yes, it is possible. The center of mass of a uniform circular ring, for example, is at the ring’s center, where there is no mass.
- The object at $300^0C$ will cool faster than the object at $100^0C$. This is in accordance with Newton’s law of cooling. As we know, rate of cooling is $\propto$ temperature between objects and its surroundings.
- For a body moving along circular path, the centripetal force acts along the radius while the displacement is tangential i.e., $\theta = 90^0$, therefore, $W=Fs\cos 90^0=0$
- The minimum possible temperature on the basis of Charle’s law is $-273.15^0C$
- 1 – (a)
2 – (c) The farther apart the people are from the pivot point, the greater the lever arm
3 – (b) Since the child on left side weigh more then the one on the right, Moment of force is more on left side in comparison to that on right side. It is easier for child on left side to lift the one on right side.
4 – (c) moment of couple = force $\times$ perpendicular distance between two forces - 1 – (c)
2 – (d)
3 – (b)
4 – (b) - Suppose the dimensions of mass $M$ be $[F^aL^bT^c]$. Then we have
$[M]=[MLT^{-2}]^a[L]^b[T]^c=M^aL^{a+b}T{-2a+c}$
equating the powers on both the sides we have
$a=1$, $a+b=0$, $-2a+c=0$
or, $b=-a=1$, $c=2a=2$
Hence dimensions of mass $M$ are $[F^1L^{-1}T^2]$
OR
Since $F=kv$
hence
$[k]=\frac{[V]}{[v^2]}=\frac{[MLT^{-2}]}{[LT^{-1}]^2}=[ML^{-1}]$ - The horizontal range of projectile is given by formula
$R=\frac{u^22\sin\theta}{g}$
(1) If angle of projection
$\theta=45^0+\alpha$ and $R=R_1$
then,
$R_1=\frac{u^22\sin(45^0+\alpha)}{g}=\frac{u^2}{g}\cos 2\alpha$
(2) If angle of projection
$\theta=45^0-\alpha$ and $R=R_2$
then,
$R_2=\frac{u^22\sin(45^0-\alpha)}{g}=\frac{u^2}{g}\cos 2\alpha$
Comparing both of them we get $R_1=R_2$ - According to the conservation of linear momentum, If the net external force acting on a system of bodies is zero, then the momentum of the system remains constant.
Condition : In order for the law of conservation of linear momentum to hold true, the system must be isolated, meaning that no external forces are acting on the objects involved in the collision or motion. - All mass of hollow cylinder lies at a distance $R$ from axis of rotation. Whereas in case of a sphere, most mass lies at a distance less than $R$ from axis of rotation.
As moment of inertia is $\sum M_iR_i^2$, so sphere has lower value of moment of inertia. - Gravitational potential energy,
$U_h=\frac{GMm}{R+h}=-\frac{gR^2m}{R+h}$
$\qquad=-\frac{mgr}{1+\frac{h}{R}}$ - Let the radius of the large drop $=R$
Radius of small drops $=r$
Volume of 27 smal drops = volume of the large drop
$\Rightarrow \qquad 27\times \frac{4}{3}\times \pi r^3=\frac{4}{3}\pi R^3$
So,
$r=\frac{R}{3}$
Surface area of large drop $=4\pi R^2$
Surface area of 27 small drops $=27\times 4\pi r^2=27\times 4\pi(\frac{R}{3})^2=12\pi R^2$
Therefore,
increase in surface area $=12\pi R^2-4\pi R^2=8\pi R^2$
Increase in energy =increase in surface area $\times$ surface tension $=8\pi R^2 \times S$ - Limitation of the first law of thermodynamics :
(i) It does not give the direction of flow of heat.
(ii) It does not explain why heat cannot be spontaneously converted into work. - Let $A$ be the displacement amplitude and $\omega$ be the angular frequency of the simple harmonic oscillator.
Then, $a_0=\omega A$ and $v_0=\omega A$
on dividing, $\frac{v_0^2}{a_0}=\frac{\omega^2A^2}{\omega^2 A}=A$
or,
$A=\frac{v_0^2}{a_0}$ - Attach the given mass $m$ to the spring and suspend the spring with the help of the scale. Restoring force of the spring is given by,
$F=-kl=-mg$ or, $\frac{m}{k}=\frac{l}{g}$
we know that time period of a vibrating system is given by,
$T=2\pi\sqrt{\frac{m}{k}}$
$\Rightarrow \qquad T=2\pi\sqrt{\frac{l}{g}}$ - $Q-CV=2.0\times 20=40\mu C=40\times 10^{-6}C$
$\frac{\Delta Q}{Q}=\frac{\Delta C}{C}+\frac{\Delta V}{V}=\frac{0.1}{2.0}+\frac{0.5}{20}=\frac{3}{40}$
$\Delta Q=\frac{3}{40} \times Q=\frac{3}{40}\times 40\times 10^{-6}=3\mu C$
Hence,
$Q=(40\pm 3.0)\times 10^{-6}C$ - Acceleration acting on the object undergoing uniform circular motion is called centripetal acceleration.
Expression : Consider a particle of mass $m$, moving with a constant speed $v$ and uniform angular velocity $\omega$, on a circular path of radius $r$ with center at $O$.
angular speed,
$\omega = \frac{\Delta \theta}{\Delta t}\qquad\qquad(1)$
let $\vec{v_1}$ and $\vec{v_2}$ be the velocity vectors. since $v=\omega r$,
$\omega\Delta t=\frac{|\Delta \vec{v}|}{|\vec{v}|}$
or,
$\frac{|\Delta \vec{v}|}{\Delta t}=|\vec{v|\omega}=(\omega r)\omega=\omega^2r$ when $\Delta t\rightarrow 0$
then
$\frac{|\Delta \vec{v}|}{\Delta t}$
represents magnitude of centripetal acceleration which is given by,
$|\vec a|=\frac{|\Delta \vec v|}{\Delta t}=\omega^2r=(\frac{v}{r})^2r$
then,
$|\vec a|=\omega^2r=\frac{v^2}{r}$ - Potential energy will increase. This is because bringing two protons closer, work has to be done against the force of repulsion. This is stored up in the form of potential energy. However, the potential energy will decrease when a proton and an electron are brought nearer. Work will be done by the force of attraction between them.
- The force on $m$ towards $M_1$ is $F=G\frac{GM_1m}{r^2}$
The force on $m$ towards $M_2$ is $F=G\frac{GM_2m}{(d-r)^2}$
Equating two forces, we have
$G\frac{GM_1m}{r^2}=G\frac{GM_2m}{(d-r)^2}$
$(\frac{d-r}{r})^2=\frac{M_2}{M_1}$ $\frac{d}{r}=\frac{\sqrt{M_2}}{\sqrt{M_1}}=\frac{\sqrt{M_2}+\sqrt{M_1}}{\sqrt{M_1}}$
So, distance of an particle from $m$ is
$r=d(\frac{\sqrt{M_1}}{\sqrt{M_2}+\sqrt{M_1}})$ - Pressure exerted by one mole of gas,
$P=\frac{1}{3}?v^2_{rms}$
$=\frac{1}{3}\frac{M}{V}v^2_{rms}$
or, $PV=\frac{1}{3}Mv^2_{rms}$
But $PV = RT$
$\frac{1}{3}Mv^2_{rms}= RT$
$Mv^2_{rms} = 3RT$
Now, average KE
$\frac{1}{3}Mv^2_{rms} = \frac{3}{2}RT$
$\frac{1}{2}(Nm)v^2 = \frac{3}{2}RT$ (? M = Nm)
$KE_{Avg}$ for one mole
$\frac{1}{3}Mv^2_{rms}= \frac{3}{2}\frac{R}{N}T= \frac{3}{2}k_BT$
? Total random K.E. for one mole $=\frac{3}{2}RT$
and average K.E. per molecule $= \frac{3}{2}k_BT$ - text books can be consulted for the answer
- text books can be consulted for the answer
- Here
$y=2 \cos 2 \pi(10 t-0.0080 x+0.35)$
$\quad =2 \cos [2 \pi(10 t-0.0080 x)+2 \pi(0.35)]$
$\quad =2 \cos \left[2 \pi \times 0.0080\left(\frac{10}{0.0080} t-x\right)+2 \pi \times 0.35\right]$
Standard equation for a travelling wave is
$y=r \cos \left[\frac{2 \pi}{\lambda}(v t-x)+\phi\right]$
Here
$\phi=\frac{2 \pi}{\lambda}x=2 \pi \times 0.008 x$
since, $\frac{2\pi}{\lambda}=0.008$
(a) when $x=4 \mathrm{~m}=400 \mathrm{~cm}$, $\phi=2 \pi \times 0.008 \times 400 =6.4 \pi \,\mathrm{rad}$
(b) when $x=0.5 \mathrm{~m}=50 \mathrm{~cm}$, $\phi=2 \pi \times 0.008 \times 50 =0.8 \pi \,\mathrm{rad}$
(c) when $x=\frac{\lambda}{2}$, $\phi=\frac{2 \pi}{\lambda} \times \frac{\lambda}{2}=\pi \,\mathrm{rad}$
(d) when $x=\frac{3}{4} \lambda$, $\phi=\frac{2 \pi}{\lambda} \times \frac{3 \lambda}{4}=\frac{3}{2} \pi \mathrm{~rad}$
 Skip to content
Skip to content
Sar muga ak physics Kia question paper with answers caia