Mathematics Important Questions for Class 12 Board 2025

Here are some good Maths important questions for Class 12 Board 2025

Question (1)

The x-coordinate of a point on the line joining the points P(2, 2, 1) and Q(5, 1, – 2) is 4. Find its z-coordinate

Question (2)

Write the principle value of  tan^-1(1) +cos^-1(-1/2)

Question (3)
A fair coin is tossed 8 times, find the probability of
(i) exactly 5 heads
(ii) at least six heads
(iii) at most six heads

Question (4)
Three cards are drawn successively with replacement from a well-shuffled pack of 52 cards. Find the mean and variance of the number of red cards

Question (5)

There are three coins. One coin is two headed coin. Second coin is biased one which comes up tail 25% times and third coin is unbiased one. One of the three coin is chosen at random and tossed and head comes. what is the probability that it was the two-headed coin?

Question (6)

Determine the values of ‘a’ and ‘b’ such that the following function is continuous
at x = 0

Question (7)

Determine the value of ‘k’ for which the following function is continuous
at x = 3 :

Question (8)

Find the value of k for which the function

is continuous at $x=\frac {\pi}{4}$

Question (9)

if x^y + y^x= a^b find dy/dx

Question (10)

Find the intervals in which the function f given by
f(x) = sin x + cos x, $0 \leq x \leq 2\pi$
is strictly increasing or strictly decreasing.

Question (11)

Question (12)

Find the intervals in which the function given by

f(x) = 2x³ – 3x² – 36x + 7 is

(a) Strictly increasing

(b) Strictly decreasing

Question (13)

Question (14)

Find the value of the below

Question (15)

If a ,b and c are mutually perpendicular vectors of equal magnitudes, find the angles which the vector 2a +b+ 2c makes with the vectors a ,b and c .

Question (16)
Solve the following linear programming problem graphically:
Minimize: z = 3x + 9y
When: $x + 3y \leq 60$
$x + y \geq 10$
$x \leq   y$
$x \geq 0$, $y \geq 0$

Question (17)

There are 4 cards numbered 1, 3, 5 and 7, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on the two drawn cards. Find the mean and variance of X

Question (18)

Using Integration, find the area of the following region

{(x, y) : $y^{^2} >ax$, $x^2+ y^2 \leq 2ax$,a > 0,$x,y \geq 0$}

Question (19)

The random variable X has a probability distribution P(X) of the following form, where k is some real number

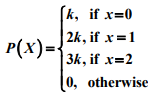
(i) Determine the value of k.
(ii) Find P (X>2)
(iii) Find P (X>2)

Question (20)

Let f : R – (-4/3) -> R be function defined as f(x)=4x/3x + 4. Show that f is a one-one
function. Also check whether f is an onto function or not. Hence find f^-1 in
(Range of f) -> R – (-4/3)

Question (21)

$\int { \frac {x^2 -1}{x^4 +1}} dx $

Question (22)

$\int {\left (\sqrt {tanx} + \sqrt {cot x} \right)} dx$

Question (23)

Find the area of the ellipse $x^2 + 9 y^2 = 36$ using integration

Question (24)

Prove that the greatest integer function defined by ?(?) = [?], 0 < ? < 2 is not differentiable at ? = 1

Question (25)

A company produces two different products. One of them needs 1/4 of an hour of assembly work per unit, 1/8 of an hour in quality control work and Rs1.2 in raw
materials. The other product requires 1/3 of an hour of assembly work per unit, 1/3 of an hour in quality control work and Rs 0.9 in raw materials. Given the
current availability of staff in the company, each day there is at most a total of 90 hours available for assembly and 80 hours for quality control. The first product
described has a market value (sale price) of Rs 9 per unit and the second product described has a market value (sale price) of Rs 8 per unit. In addition, the maximum amount of daily sales for the first product is estimated to be 200 units, without there being a maximum limit of daily sales for the second product.
Formulate and solve graphically the LPP and find the maximum profit

Question (26)

In an elliptical sport field the authority wants to design a rectangular soccer field with the maximum possible area. The sport field is given by the graph of
$ \frac {x^2}{a^2} + \frac {y^2}{b^2} =1$
(i) If the length and the breadth of the rectangular field be 2x and 2y respectively, then find the area function in terms of x.
(ii) Find the critical point of the function.
(iii) Use First derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.
OR
(iii) Use Second Derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.

Related Articles

Class 12 Maths Syllabus( Latest)
Definite integration formulas
Integrals class 12 important questions