Domain and Range Of Inverse Trigonometric Functions

Inverse trigonometric functions are the inverse functions of the basic trigonometric functions: sine, cosine, and tangent. To define these inverse functions, we need to restrict the domain and range of the original functions so that they become one-to-one and onto.

Here are the domain and range for each of the primary inverse trigonometric functions:

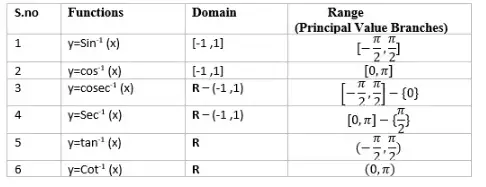
1. Inverse Sine function ($sin^(-1)$ or arcsin):

Domain: $-1 \leq x \leq 1$, as the sine function takes values in this range.

Range: $-\pi/2 \leq y \leq \pi/2$, which corresponds to the interval over which sine is a strictly increasing function.

2. Inverse Cosine function ($cos^(-1)$ or arccos):

Domain: $-1 \leq x \leq 1$, as the cosine function takes values in this range.
Range: $0 \leq y \leq \pi$, which corresponds to the interval over which cosine is a strictly decreasing function.

3. Inverse Tangent function ($tan^(-1)$ or arctan):

Domain: $-\infty < x < \infty$, as the tangent function takes values over the entire real line.
Range: $-\pi/2 < y < \pi/2$, which corresponds to the interval over which tangent is a strictly increasing function.

There are also three other inverse trigonometric functions corresponding to the reciprocal functions of sine, cosine, and tangent: inverse cosecant, inverse secant, and inverse cotangent. Their domain and range are as follows:

4. Inverse Cosecant function ($csc^(-1)$ or arccsc):

Domain: $x \geq -1$ or $x \geq 1$, as the cosecant function takes values in this range.
Range: $-\pi /2 \leq y < 0$ or $0 < y \leq \pi/2$, which corresponds to the interval over which cosecant is a strictly decreasing function.

5. Inverse Secant function ($sec^(-1)$ or arcsec):

Domain: $x \leq -1$ or $x \geq 1$, as the secant function takes values in this range.
Range: $0 \leq y < \pi/2$ or $\pi/2 < y \leq \pi$, which corresponds to the interval over which secant is a strictly decreasing function.

6. Inverse Cotangent function ($cot^(-1)$ or arccot):

Domain: $-\infty < x < \infty$, as the cotangent function takes values over the entire real line.
Range: $0 < y < \pi$, which corresponds to the interval over which cotangent is a strictly decreasing function.

How to remember it

• The domain of the inverse function is the range of the original trigonometric function
• The range of the Inverse function is the smallest interval in which it becomes one-one and onto.lets see how we can remember it

Lets first rewrite the table in below manner

We can use below tricks to remember the range base on this

• We can clearly see that inverse of sin, cosec and tan have a similar type of range while inverse of cos ,sec and cot having similar type of range
• sin and cosec but it exclude 0 as then it will become undefined, Similar for cos and sec
• inverse of tan and cot are in different interval