How to calculate percentage error

In this article, we will discuss how to calculate percentage error and this applies to measurements in both physics and chemistry. Both physics and chemistry are sciences that depend on measurements. While doing experiments it is expected that we get values that are accurate but our instruments have limitations. Since our instruments are not accurate we get errors in measurements. This error is the difference between the true/accepted value and the measured/experimental value.

Meaning of percentage error

Percent errors mean how accurate our results are when we measure something. Smaller percentage errors mean that we are close to the true/accepted value. A 2% error, for instance, suggests that we got quite close to the true value, while 50% means our results are not accurate and nowhere close to the true value.

In measurement errors are often unavoidable due to certain reasons like lack of skill of the person doing the measurement, limitations of measuring instruments, or some external factors beyond our control. The percent error formula will tell us how seriously these inevitable errors have influenced our results. Since this article is about percentage error let us now define it.

Definition

Percentage error definition:

Percent error is the difference between the measured value and the true value, as a percentage of true value.

We use Percentage Error to compare a measured or experimental value to a true or accepted value value. This helps you to see how far away the measured value or the value you estimated is in comparison to the true value or the accepted value.

Formula

Percentage error formula is $$\text{Percentage Error}= \frac{|\text{Measured Value}-\text{True Value}|}{|\text{True Value}|}\times 100$$
Or,
$\text{% Error}=\frac{|T-M|}{|T|}\times 100$
Where,
$T=$ true/accepted value
$M=$ measured/experimental value
Also, here the symbol “|” means absolute value where negative becomes positive.

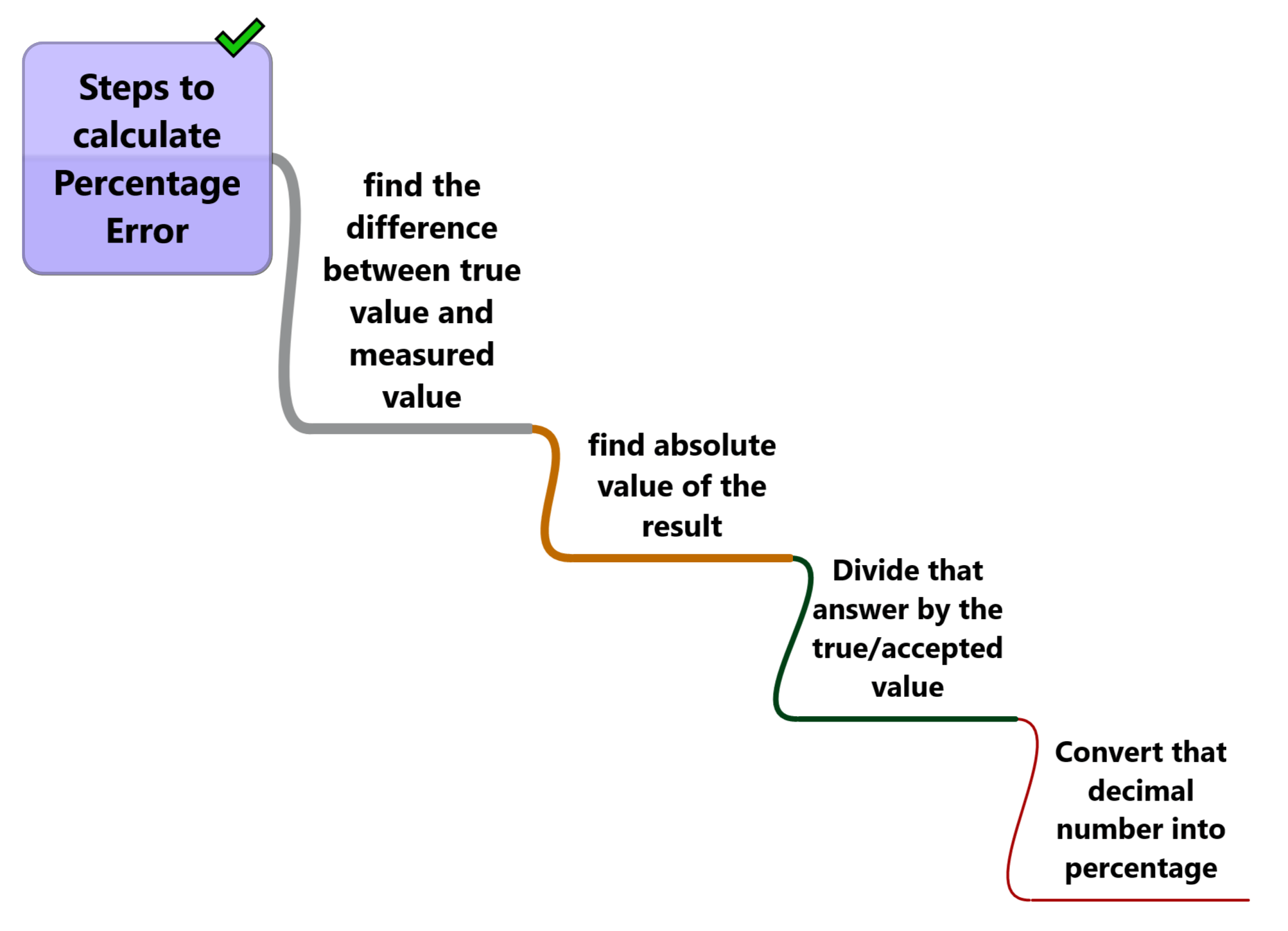
Steps for calculating percentage error

The following are the steps you can follow for calculating percentage error when you have information about the measured value and true/accepted value of a physical or chemical quantity.

1. First, find the difference between the true value and the measured value.
2. Now find the absolute value of the result of the first step.
3. Divide that answer by the true/accepted value and you will get a decimal number
4. Convert that decimal number into a percentage (multiply that answer by 100 and add the % symbol ). Now that we know the steps involved for calculation let us have a look at some examples to clarify the concept.

Percentage error example

Example 1

A student measures the radius of a circular sheet of paper and finds that it is 15 cm long. The label on the package indicates that the radius is is 17 cm. Calculate the percentage error in the measurement.

Solution:
Measured value = 15 cm
Accepted value = 17 cm
Step 1: Subtract the measured value from the accepted value.
17 cm – 15 cm = 2 cm
Step 2: Take the absolute value of step 1
|2 cm| = 2 cm
Step 3: Divide that answer by the accepted value.
$\frac{2 cm}{17 cm}=0.12$ (by rounding off to two significant figures)
Step 4: Multiply that answer by 100 and add the % symbol to express the answer as a percentage.
0.12 x 100 = 12%
The percent error of the measurement was 12%.

Example 2

Suki weighed an object on her balance and recorded a mass of 13.62 grams. Her teacher told her that there was obviously something wrong with her balance because it was giving her a reading which was 22.22% too high. Find the actual mass of the object.
Solution:
Our previous question was a straightforward question where you just have to put in the values and calculate the percentage error.
In this question, we are given the mass of the object and the percentage error. Here we have to calculate the actual mass of the object.
So,
Measured value = 13.62 grams
percentage = 22.22%
$\text{Percentage Error}= \frac{|\text{Measured Value}-\text{True Value}|}{|\text{True Value}|}\times 100$
Putting in the values we get
$22.22=\frac{M-T}{T}\times 100$
$\frac{22.22T}{100}=M-T$
$1.2222T=M$
Given that $M=13.62 gm$ and putting in the value of $M$ in the above formula we get
$T=\frac{M}{1.2222}=\frac{13.62}{1.2222}=11.143\ gm$
Which is the true/actual mass.
So here we have to rearrange the formula to calculate the desired quantity.

Can percentage error be negative?

Percentage error is typically taken as a positive value because the magnitude of the error is what’s crucial, not its direction. However, specific fields like chemistry sometimes require the sign of the error to be indicated.

In such cases, you don’t use the absolute difference between two values. The sequence of subtraction is essential: subtract the measured value from the true value. If the percentage error is negative, it means the measured value exceeds the true or accepted value.

Unless specifically needed, it’s standard practice to use the absolute value and report the percentage error as a positive number.

For instance, let’s say you estimated a board’s length at 22 cm, while a colleague measured it as 18 cm. To determine the percentage error for both measurements, you need the “true” or “accepted” value. After consulting the manufacturer’s documentation, you find the board is 20 cm long, which serves as the accepted value.

Here’s how you calculate the percentage error for both measurements:

Formula:
\[ \text{Percentage Error} = \frac{|\text{Measured Value} – \text{True Value}|}{|\text{True Value}|} \times 100 \]

For your measurement:
\[ \text{Percentage Error} = \frac{22 – 20}{20} \times 100 = 10% \]
Result: +10%

For your colleague’s measurement:
\[ \text{Percentage Error} = \frac{18 – 20}{20} \times 100 = -10% \]
Result: -10%

In this example, your colleague’s error is below the accepted value (negative), while yours is above (positive).

What is a good percent error

The amount of error that is appropriate or good, varies with the case under consideration. Suppose you calculate the distance between New Delhi and Gurugram on a map and you estimate it to be around 25 Km. If the actual distance is 30 Km, the chances are that the trip between the two cities would have little impact on this mistake. But if the calculations used to send satellites to designated orbit were to have the same degree of error, then whole mission would be in trouble.

Further Reading

• https://www.youtube.com/watch?v=JbEo46uV6d4 :- very simple and basic explanation of the concept.
• Weight Percent Formula | How to convert weight percent to mole fraction