How to easily remember trigonometric ratios table (0-90)

Trigonometry is a branch of mathematics that deals with the study of triangles and the relationships between their sides and angles. One of the fundamental concepts in trigonometry is trigonometric ratios, which are ratios of the sides of a right triangle to its angles. There are six trigonometric ratios – sine, cosine, tangent, cosecant, secant, and cotangent – that are used to solve problems related to angles, distances, and heights. In this article, we will discuss a trigonometric ratios table that can help students understand these ratios easily.

Trigonometric ratios table

Trigonometric ratios table for standard angles (0-90) is given as

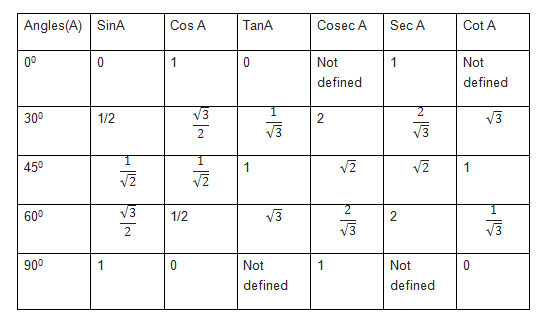
Students often find it difficult to remember and use it trigonometric equations, questions and problems

There is one easy way to remember these trigonometric ratios table.Lets check it out

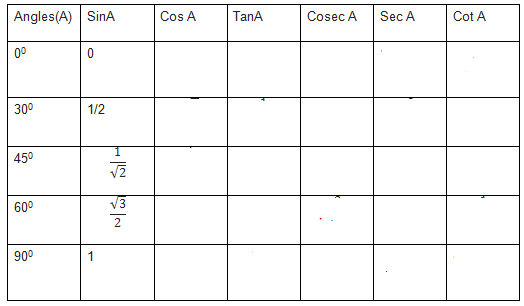
1.For sin ratios for 0,30 ,45 ,60 and 90, we can remember them as by taking square root of the fraction of 0/4,1/4,2/4,3/4,4/4

$sin 0 = \sqrt { \frac {0}{4}} = 0$

$sin 30 = \sqrt {\frac  {1}{4}} = 1/2$

$sin 45 = \sqrt {\frac {2}{4}} = \frac {1}{ \sqrt {2}}$

$sin 60 = \sqrt { \frac {3}{4}} = \frac {\sqrt {3}}{2}$

$sin 90 = \sqrt {\frac {4}{4}} =1$

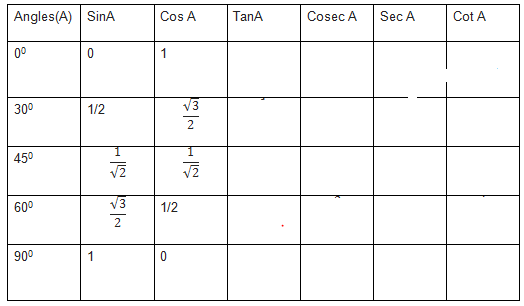
2.for cos ratios for 0,30 ,45 ,60 and 90, we can remember them as opposite order from sin 90 to 0

$cos 0 = sin 90 =1$

$cos 30 =sin 60 = \frac {\sqrt {3}}{2}$

$cos 45= sin45 =\frac {1}{ \sqrt {2}}$

$cos 60 =sin 30 = 1/2$

$cos 90 =sin 0 =0$

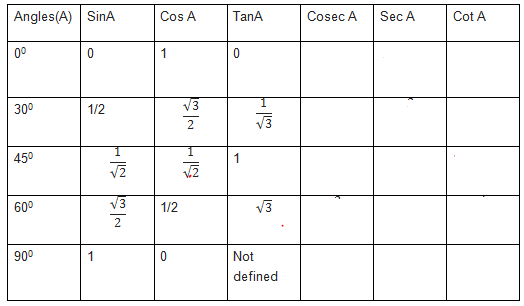
3.for tan ratios for 0,30 ,45 ,60 and 90, we can remember them as

$tan x = \frac {sin x}{cos x}$

$tan 0 = 0/1 =0$

$tan 30 =  \frac {sin 30}{cos 30}= \frac {1}{ \sqrt {3}}$

$tan 45 =  \frac {sin 45}{cos 45}= 1$

$tan 60 =  \frac {sin 60}{cos 60}= \sqrt {3}$

$tan 90 = \frac {sin 90}{cos 90}= 1/0$ .This is undefined

(4) For cosec ratios for 0,30 ,45 ,60 and 90, we can remember them as

$cosec A = \frac {1}{sinA}$

$cosec 0 = 1/0$ .This is undefined

$cosec 30 = \frac {1}{sin30} =2$

$cosec 45 = \frac {1}{sin45} =\sqrt {2}$

$cosec 60 = \frac {1}{sin60} =\frac {2} {\sqrt {3}}$

$cosec 90 = \frac {1}{sin90} =1$

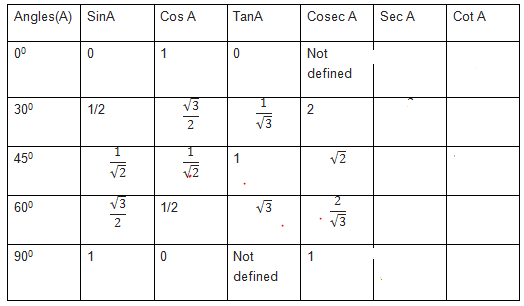
5.for sec ratios for 0,30 ,45 ,60 and 90, we can remember them as

$sec A = \frac {1}{cosA}$

$sec 0 = 1$ .

$sec 30 = \frac {1}{cos30} =\frac {2} {\sqrt {3}}$

$cosec 45 = \frac {1}{cos45} =\sqrt {2}$

$cosec 30 = \frac {1}{sin60} =2$

$cosec 90 = \frac {1}{cos90} =1/0$. This is undefined

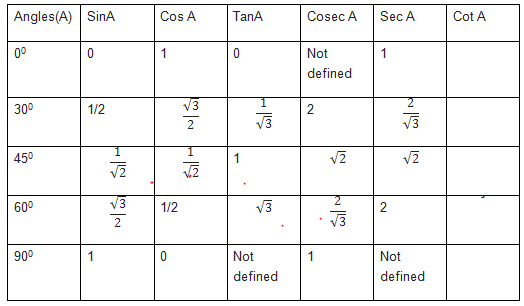
6.for cot ratios for 0,30 ,45 ,60 and 90, we can remember them as

$cot x = \frac {cos x}{sin x}$

$cot 0 = 1/0$ This is undefined

$cot 30 =  \sqrt {3}$

$cot 45 =  1$

$tan 60 =  \frac {1}{ \sqrt {3}}$

$cot 90 = \frac {cos 90}{sin 90}= 0$ .

Benefits of Trigonometric Ratios Table:

• The trigonometric ratios table is a useful tool for students as it provides an easy way to understand the six trigonometric ratios for different angles.
• This table will help student to solve problems related to trigonometry.
• The table also highlights the undefined values for some ratios, such as cosecant and secant for 0° and 90°, which helps in avoiding errors while solving problems.

Frequently Asked Questions:

Q. How can I remember the trigonometric ratios?

A. One way to remember the trigonometric ratios is by memorizing the acronym “SOHCAHTOA,” where S stands for sine, C stands for cosine, T stands for tangent, O stands for opposite, A stands for adjacent, and H stands for hypotenuse. The acronym can help in remembering the ratios and their definitions.

Q. What is the value of tangent for 45°?

A. The value of tangent for 45° is 1.

Q. How is trigonometry used in real life?

A. Trigonometry is used in various fields such as architecture, engineering, surveying, navigation, and physics to calculate distances, heights, and angles

Related Articles

Trigonometric table from 0 to 360
Trigonometry Formulas for class 11 (PDF download)
trigonometric formulas for Class 10
Important trigonometry questions for class 11 Maths
Ncert solutions for class 10 maths