Trigonometry Formulas for class 11
(PDF download)
Trigonometry is quite an interesting subject. Here are the useful Trigonometry Formulas for class 11 Maths
Basic Formula
$tan(x) = \frac {sin(x)}{cos(x)}$
$cot(x) = \frac {cos(x)}{sin(x)}$
Reciprocal Identities:
$cosec(x) = \frac {1}{sin(x)}$
$sec(x) =\frac { 1}{cos(x)}$
$cot(x) = \frac {1}{tan(x)}$
$sin(x) = \frac {1}{cosec(x)}$
$cos(x) = \frac {1}{sec(x)}$
$tan(x) = \frac {1}{cot(x)}$
Pythagorean Identities:
$sin^2(x) + cos^2(x) = 1$
$cot^2x +1 = cosec^2x$
$1+tan^2x = sec^2x$
Trigonometric Ratio’s of Common angles
We can find the values of trigonometric ratio’s various angle
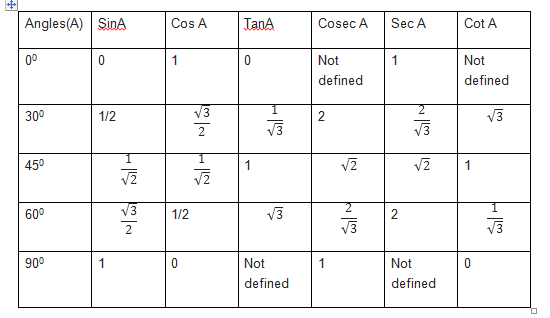
Trigonometry Formula for Complementary and supplementary angles
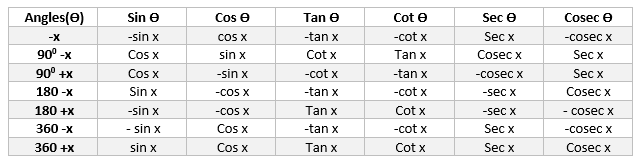
Sin and cos function
- $cos(A+B)=cos(A)cos(B)-sin(A)sin(B)$
- $cos(A-B)=cos(A)cos(B)+sin(A)sin(B)$
- $cos(\pi /2 -A)=sin(A)$
- $sin(\pi /2 -A)=cos(A)$
- $sin(A+B)=sin(A)cos(B)+sin(B)cos(A)$
- $sin(A-B)=sin(A)cos(B)-sin(B)cos(A)$
Tan and cot functions
If none of the angles x, y and (x + y) is an odd multiple of $\pi /2$
$tan(A+B)=\frac{tan(A)+tan(B)}{1-tan(A)tan(B)}$
$tan(A-B)=\frac{tan(A)-tan(B)}{1+tan(A)tan(B)}$
If none of the angles x, y and (x + y) is a multiple of $\pi /2$
$cot(A+B)=\frac{cot(A)cot(B)-1}{cot(A)+cot(B)}$
$cot(A-B)=\frac{cot(A)cot(B)+1}{cot(B)-cot(A)}$
Some more Trigonometric Functions
Double of x (Double Of Angles)
$cos2x=cos^{^{2}}x-sin^{^{2}}x=2cos^{^{2}}x-1=1-2sin^{^{2}}x=\frac{1-tan^{^{2}}x}{1+tan^{^{2}}x}$
$sin2x=2cos(x)sin(x)=\frac{2tan(x)}{1+tan^{^{2}}x}$
$tan2x=\frac{2tan(x)}{1-tan^{^{2}}x}$
Triple of x ( Triple of Angles)
$sin3x=3sin(x)-4sin^{3}x$
$cos3x=4cos^{3}x-3cos(x)$
$tan(3x)=\frac{3tanx-tan^{^{3}}x}{1-3tan^{^{2}}x}$
Sum and Difference of Angles
$cos(A)+cos(B)=2cos\frac{A+B}{2}cos\frac{A-B}{2}$
$cos(A)-cos(B)=-2sin\frac{A+B}{2}sin\frac{A-B}{2}$
$sin(A)+sin(B)=2sin\frac{A+B}{2}cos\frac{A-B}{2}$
$sin(A)-sin(B)=2cos\frac{A+B}{2}sin\frac{A-B}{2}$
Half Angle Formula
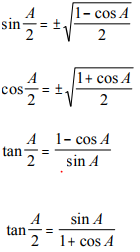
Pythagoras’ Identities in Radical form
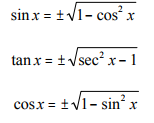
Power Reducing Functions
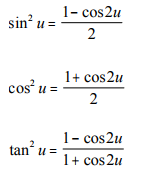
Trigonometric equations Formula’s
1.$sin x = 0$ implies $x = n \pi$, where n is any integer<br>
2.$cos x = 0$ implies $x = (2n + 1)(\pi /2)$<br>
- $sinx =siny$ then $x=n \pi + (-1)^{n}y$ where n is any integer<br>
- $cosx=cosy$ then $x=2n \pi + y$ or $x=2n \pi – y$ where n is any integer<br>
- $tanx=tany$ then $x=n \pi +y$ where n is any integer<br>
5. Equation of the form
$sin^2x = sin^2 y, cos^2 x = cos^2 y , tan^2 x = tan^2 y$
The general solution is given by
$x = n \pi \pm y$ where n is any integer
6. Equation of the Form
|sin x|=1 ,General solution is given by $x= (2n+1) \frac {\pi}{2}$<br>
|cos x|=1, general solution is given by $x=n \pi$<br>
Some basics Tips to solve the trigonometry questions
(1) Always try to bring the multiple angles to single angles using the basic formula. Make sure all your angles are the same. Using $sin(2x)$ and $sin(x)$ is difficult, but if you use $sin(2x) = 2 sin(x)cos(x)$, that leaves $sin(x)$ and $cos(x)$, and now all your functions match. The same goes for addition and subtraction: don’t try working with $sin(x+y)$ and $sin (x-y)$. Instead, use $sin(X+Y) = sin(x)cos(y)+cos(x)sin(y)$ so that all the angles match
(2) Converting to sin and cos all the items in the problem using a basic formula. I have mentioned sin and cos as they are easy to solve. You can use any other also.
(3)Check all the angles for sums and differences and use the appropriate identities to remove them.
(4) Use Pythagorean identifies to simplify the equations
(5) Practice and Practice. You will soon start figuring out the equation and their symmetry to resolve them fast
Download all the trigonometry Formulas below
Hope you like this compilation of Trigonometry Formulas for class 11. This will be very useful for the Maths students
Download Trigonometry Formulas PDF
Related Links
Trigonometric functions
Domain ,Range and Graphs of Trigonometric functions
Trigonometric equations
sin cos tan table
Important trigonometry questions for class 11 Maths
how to remember trigonometry table easily
https://en.wikibooks.org/wiki/Trigonometry/Remembering_Trig_Formulae
Of great help. If only can be made in down loadable PDF format..
Hi pdf download is available after related links at the end of the article. I’ll highlight it so that it become more visible. Thanks
Trigonometry
6×cos2x+sin2x
this compilation of formulas was really helpfull. In my opinion some examples should also be added in order to clear some basic doubts.
Will appreciate to be explained which formula or identity to use and when solving equations.
Thnaks and looking forward to hear from you soon.
Helful formula.
Sir great help….
Pls tell ur name
Very good website
sir it would be great if a last summery page of main formulas to be added
This website is helfpul for all the students