This article is about Coordinate transformation . In this article we will look at coordinate transformation in case of translation, inclination and rotation of S' frame of reference with respect to S frame of reference. This article is mainly for B.Sc. first year and comes under subject Mechanics.
Coordinate transformation
If we define the position of a particle in two different frames of then in both the cases projection of the particle comes out to be different and the relation between the projections of this particle in two different frames of reference is known as their transformation equations.
If there is no relative velocity between the frames of references and they rotate through a certain degree then the transformation does not depend on time. Opposite to this when there is a certain relative velocity between them then transformation equation depends on time.
Transformation equations for frames of reference involving translation
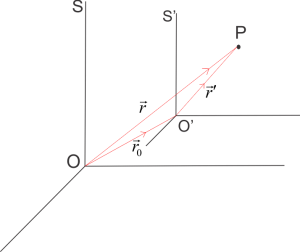
Consider two frames of reference S and S’ whose origins are O and O’ and observers are at the point O and O’ as shown below in figure 1. If the position vector of any point P in S is $\vec{r}$ then its position vector in S’ would be $\vec{r’}$.
According to figure
$\overrightarrow{r’}=\vec{r}-\overrightarrow{{{r}_{0}}}$
Differentiating it w.r.t. time
$\frac{\vec{r’}}{dt}=\frac{\vec{r}}{dt}-\frac{\vec{r_0}}{dt}$
If $\vec{r_0}$ is constant then
$\frac{d\vec{r_0}}{dt}=0$
Therefore,
$\frac{d\vec{r}}{dt}=\frac{d\vec{{r}’}}{dt}$
$\vec{v}=\vec{v’}$
Again differentiating it w.r.t. time
$\frac{d\vec{v}}{dt}=\frac{d\vec{{v}’}}{dt}$
Or,
$\vec{a}=\vec{a’}$
So, in translated frame of reference S’ the position of the particle would be different but the acceleration and velocity would be same as measured in S frame of reference. Also the equations 1, 2 and 3 are time independent equations.
Coordinate transformations in reference frames having uniform relative translational motion
In figure 1 if the frame of reference S’ has translational motion with constant velocity w.r.t. the frame of reference S than at any time their axis would be at a constant distance but the position would depend on time. If in the beginning at $t=0$ both the frame of reference has origin O and O’ at the same point. Now at time t position vector of O’ w.r.t. O would be
$\vec{r_0}=\vec{v}t$
Hence
$\vec{r’}=\vec{r}-\vec{r_0}$
$\vec{r’}=\vec{r}-\vec{v}t$
Differentiating it w.r.t. the time we get
$\vec{v’}=\frac{d\vec{r}}{dt}-\frac{d\vec{r_0}}{dt}=\vec{u}-\vec{v}$
Acceleration of the particle
$\vec{{a}’}=\frac{d\vec{u}}{dt}-\frac{{\vec{v}}}{dt}=\vec{a}$
As $\vec{v}$ is constant.
Hence the position and velocity of the particle could change according to equations 4 and 5 when it is moving with uniform relative motion but acceleration remains unchanged.
Equations 4, 5 and 6 are time-dependent transformation equations.
Transformation in an inclined frame of reference
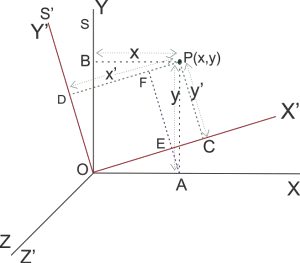
Let x, y, z, be the coordinates of a particle in a frame of reference say S as shown in figure 2.
So we have,
\begin{equation}
\label{eq:1}
x=PB=OA \\
y=PA=OB
\end{equation}
Another frame of reference S’ is inclined w.r.t. the frame of reference S such that the origins of both the frame of reference and their z-axis coincide as shown in figure 2.
Now coordinates of point P in S’ frame of reference would be
\begin{equation}
\label{eq:2}
X’=PD=OC \\
Y’=PC=OD
\end{equation}
Since z and z’ coincides we have
\begin{equation}
\label{eq:3}
z=z’
\end{equation}
Now from right angle $\bigtriangleup OAE$ we have
\begin{equation*}
\frac{OE}{OA}=cos\theta \qquad\text{or}\qquad OE=xcos\theta \\
\frac{AE}{OA}=sin\theta \qquad\text{or}\qquad AE=xsin\theta
\end{equation*}
Again from right angle $\bigtriangleup FAP$ we have
\begin{equation*}
\frac{AF}{AP}=cos\theta \qquad\text{or}\qquad AF=ycos\theta \\
\frac{PF}{AP}=sin\theta \qquad\text{or}\qquad PF=ysin\theta
\end{equation*}
now,
\begin{equation*}
x’=PD=PF+FD \\
\text{or,} \\
x’=PF+OE
\end{equation*}
This implies that,
\begin{equation}
\label{eq:4}
x’=xcos\theta+ysin\theta
\end{equation}
Similarly,
$$y’=PC-EF = AF-AE$$
\begin{equation} \label{eq:5}
y’=ycos\theta -xsin\theta
\end{equation}
Equations (\ref{eq:4}) and (\ref{eq:5}) can also be written as
\begin{equation}
\label{eq:6}
x’=xcos(X’OX)+ycos(X’OY)
\end{equation}
\begin{equation}
\label{eq:7}
y’=xcos(Y’OX)+ycos(Y’OY)
\end{equation}
Equations (\ref{eq:4}) ,and (\ref{eq:5}) ,(\ref{eq:6}) and (\ref{eq:7}) are the transformation equations for an inclined frame of reference.
Three dimensional coordinate transformation
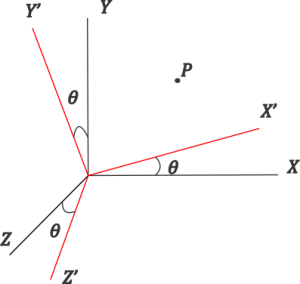
If all the axis of the frame of reference $S’$ are inclined to frame of reference $S$ through an angle $\theta$ then coordinate transformation of the frame of reference is done through the following rule
\begin{align}
x’=xcos(X’OX)+ycos(X’OY)+zcos(X’OZ)\\
y’=xcos(Y’OX)+ycos(Y’OY)+zcos(Y’OZ)\\
Z’=xcos(Z’OX)+ycos(Z’OY)+zcos(Z’OZ)
\end{align}
If the unit position vectors of $x, y, z$ are $\hat i, \hat j, \hat k$ and of of $x’, y’, z’$ are $\hat i’, \hat j’, \hat k’$ then
\begin{equation*}
X’OX=\hat i’ \cdot \hat i = a_{11}\\
X’OY=\hat i’ \cdot \hat j = a_{12}\\
X’OZ=\hat i’ \cdot \hat k = a_{13}\\
Y’OX=\hat j’ \cdot \hat i = a_{21}\\
Y’OY=\hat j’ \cdot \hat j = a_{22}\\
Y’OZ=\hat j’ \cdot \hat k = a_{23}\\
Z’OX=\hat k’ \cdot \hat i = a_{31}\\
Z’OY=\hat k’ \cdot \hat j = a_{32}\\
Z’OZ=\hat k’ \cdot \hat k = a_{33}
\end{equation*}
hence,
\begin{align}
x’=a_{11}x+a_{12}y+a_{33}z \label{eq:12}\\
y’=a_{21}x+a_{22}y+a_{23}z \label{eq:13}\\
z’=a_{31}x+a_{32}y+a_{33}z \label{eq:14}
\end{align}
In the form of matrix
\begin{equation}
\begin{bmatrix}
x’\\
y’\\
z’
\end{bmatrix}=\begin{bmatrix}
a_{11} &a_{12} &a_{13} \\
a_{21}&a_{22} &a_{23} \\
a_{31}&a_{32} & a_{33}
\end{bmatrix}+\begin{bmatrix}
x\\
y\\
z
\end{bmatrix}
\end{equation}
Direction cosines of $3 \times 3 $ matrix is
\begin{equation}
\begin{bmatrix}
a_{11} &a_{12} &a_{13} \\
a_{21}&a_{22} &a_{23} \\
a_{31}&a_{32} & a_{33}
\end{bmatrix}
\end{equation}
This matrix is also known as rotation matrix.
Transformation of velocity
By differentiating transformation equations with respect to time we would get velocity components in $S’$ frame of reference. So,
\begin{align}
v’_x =\frac{dx’}{dt} =a_{11}\frac{dx}{dt}+a_{12}\frac{dy}{dt}+a_{13}\frac{dz}{dt}=a_{11}v_x+a_{12}v_y+a_{13}v_z\\
v’_y =\frac{dy’}{dt} =a_{21}\frac{dx}{dt}+a_{22}\frac{dy}{dt}+a_{23}\frac{dz}{dt}=a_{21}v_x+a_{22}v_y+a_{23}v_z\\
v’_z =\frac{dz’}{dt} =a_{31}\frac{dx}{dt}+a_{32}\frac{dy}{dt}+a_{33}\frac{dz}{dt}=a_{31}v_x+a_{32}v_y+a_{33}v_z
\end{align}
Transformation of acceleration
Differentiating equations of velocity w.r.t. $t$ we get
\begin{align}
a’_x =\frac{d^2x’}{dt^2} =a_{11}\frac{d^2x}{dt^2}+a_{12}\frac{d^2y}{dt^2}+a_{13}\frac{d^2z}{dt^2}=a_{11}a_x+a_{12}a_y+a_{13}a_z \label{eq:20}\\
a’_y =\frac{d^2y’}{dt^2} =a_{21}\frac{d^2x}{dt^2}+a_{22}\frac{d^2y}{d^2t}+a_{23}\frac{d^2z}{dt^2}=a_{21}a_x+a_{22}a_y+a_{23}a_z \label{eq:21}\\
v’_z =\frac{d^2z’}{dt^2} =a_{31}\frac{d^2x}{dt^2}+a_{32}\frac{d^2y}{dt^2}+a_{33}\frac{d^2z}{dt^2}=a_{31}a_x+a_{32}a_y+a_{33}a_z \label{eq:22}
\end{align}
If $S$ frame of reference is an inertial frame of reference and no force is acting on point $P$ then
$$\frac{d^2x}{dt^2}=\frac{d^2y}{dt^2}=\frac{d^2z}{dt^2}=0$$
Putting it in equations (\ref{eq:20}) ,(\ref{eq:21}) and (\ref{eq:22})
$$\frac{d^2x’}{dt^2}=\frac{d^2y’}{dt^2}=\frac{d^2z’}{dt^2}=0$$
This implies that frame of reference $S’$ is also an inertial frame of reference and equations (\ref{eq:12}) ,(\ref{eq:13}) and (\ref{eq:14}) are time independent transformation equations of coordinates of rotating frame of reference.
Physics for Degree Students B.Sc. First Year
Mechanics: For Students of B.Sc (Pass and Hons.): D.S. Mathur
An Introduction to Mechanics (SIE) by David Kleppner, Robert Kolenkow
Texts
1st Law and Newtonian space and time.
Absolute time and space