Position of a particle (Mechanics)

This article " Position of a particle " is for B.Sc. students. We have also defined inertial and non inertial frame of reference in this article.

Position of a particle

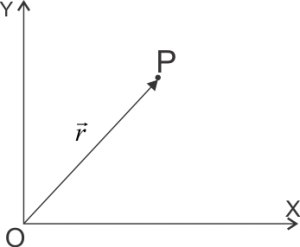
(a) By Position Vector:-

The line joining the point P and the origin ‘O’ of the frame of reference that is $\vec{PO}$ is known as position vector and is also represented by $\vec{r}$.

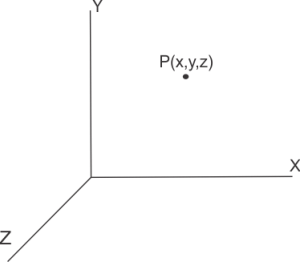
(b) By coordinates:-

The position of a point P can also be represented in the coordinate system in the form of mutually perpendicular x, y, and z axis.

Position of a moving particle

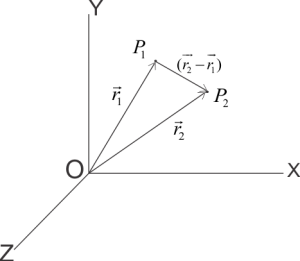
If any point changes its position from $P_1}$ to $P_2$ with respect to time then position vector of point will be $\vec{r}$ at time $t$ and its displacement vector would be given by

$\vec{P_1P_2}=(\vec{r_2}-\vec{r_1})$

Where $P_1$ and $P_2$ is the position of moving particle at time $t_1$ and $t_2$ and  $\vec{r_1}$ and $\vec{r_2}$ are position vectors at time $t_1$ and $t_2$ .

Now time interval is

$\Delta t={{t}_{2}}-{{t}_{1}}$

Displacement of the particle is given by

$\Delta \vec r = \overrightarrow {{r_2}}  – \overrightarrow {{r_1}} $

Rate of change of position or velocity is given by

$\vec{v}=\frac{\vec{r_2}-\vec{r_1}}{t_2 – t_1}=\frac{\Delta \vec{r}}{\Delta t}$

If time interval is very very less i.e. $\Delta t\to 0$ then the change in position with respect to time is called instantaneous velocity.

Or,

$\vec{v}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta \vec{r}}{\Delta t}$

By the definition of differentiation

$\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta \vec{r}}{\Delta t}=\frac{d\vec{r}}{dt}$

If the velocity of particle is changing with respect to time then this is called rate of change of velocity or acceleration. Let $\vec{v_1}$ and $\vec{v_2}$ be the velocities of particle at time $t_1$ and $t_2}$ respectively then,

Change in velocity = $\vec{v_2}-\vec{v_1}=\Delta \vec{v}$

Change in time = $t_2 – t_1 = \Delta t$

Rate of change of velocity would be

$\vec{a}=\frac{\overrightarrow{{{v}_{2}}}-\overrightarrow{{{v}_{1}}}}{{{t}_{2}}-{{t}_{1}}}=\frac{\Delta \vec{v}}{\Delta t}$   

If time interval is very very less i.e. $\Delta t\to 0$ then the change in velocity with respect to time is called instantaneous acceleration i.e.,

$\vec{a}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta \vec{v}}{\Delta t}=\frac{d}{dt}\left( \frac{d\vec{r}}{dt} \right)=\frac{{{d}^{2}}\vec{r}}{d{{t}^{2}}}$

Inertial and Non-Inertial frame of reference

Frames of reference are of two types

(1) Inertial frame of reference

(2) Non Inertial frame of reference

1. Inertial frame of reference:-

If no external force is acting on the particle then the frame of reference with respect to which the particle seems to be moving at constant velocity or with no acceleration is known as inertial frame of reference. Since no external force is acting on the particle we have

$\vec{F}=m\frac{d^2 \vec{r}}{dt^2}=0$

Therefore, acceleration

$\vec{a}=\frac{d^2 \vec{r}}{dt^2}=0$

or, velocity

$v=constant$

Clearly in absence of external force the particle will move with a constant velocity in the frame of reference. Therefore for inertial frame of reference Newton’s first and second laws of motion are always valid. By analysis it is found that such frames are either at rest or move with constant velocity. Hence for an observer at rest or moving with constant velocity frame of reference are always inertial frames of reference.

2. Non-inertial frame of reference:-

 

In non-inertial frame of reference Newton’s first and second laws of motion does not holds true. In non-inertial frame of reference observer or frame of reference accelerates and particle or object observed relative to them seems to be accelerated in the absence of any externally applied force.

In this article we have covered how to define Position of a particle. For further reference you can visit the links given below