Galilean transformations

[latexpage]
Motion is a relative concept. You are sitting on a train. An object on trains seems to be at rest from your perspective but it is in motion from the person standing on the ground. So it is tied to a particular frame of reference chosen by observer.
Now Different observer may use the different frame of reference, And velocity, acceleration may be different from these different frames of reference
It is important to know how these measurements in a different frame of reference are related.

We can easily prove that Newton’s equations of motion, if they hold in any coordinate system, also hold in any other coordinate system translating uniformly w.r.t. the first frame of reference. This is the Newtonian principle of relativity.
Galilean transformations are a set of equations that relate the space and time coordinates of two systems which are moving at a constant velocity relative to each other. These transformation equations describe the phenomenon when speeds involved are much less than the speed of light. It assumes space and time to be absolute. According to these equations mass, time and length do not depend on the relative motion of the observer.

Transformation of Position

Let the position vector of point $P$ w.r.t. the frame of reference $S$ is $\vec r$ and if its coordinates are $x$, $y$ and $z$ then,
\begin{equation}
\vec{OP}=\vec{r} = x \hat{i} + y \hat{j} + z \hat{k}
\end{equation}
where $\hat i$. $\hat j$ and $\hat k$ are unit vectors.

(a) When both the coordinates coincide with each other at $t=0$

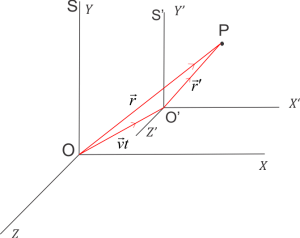
Consider two frames of reference $S$ and $S’$ which coincides with each other at time $t=0$. Let $S’$ is moving with a constant velocity $\vec v$ such that axis of $S’$ i.e., $X’$. $Y’$ and $Z’$ remains parallel to the axis of frame $S$ i.e., $X$, $Y$ and $Z$.
Now at time $t$ the position vector of origin of $S’$ with respect to $O$ be
$OO’=\vec v t$
At this time position vector of $P$ in $S’$ would be $\vec {r’}$ and its coordinates would be $x’$. $y’$ and $z’$.
Position of particle w.r.t. $S$ frame of reference is,
\begin{equation}
\vec{O’P}=\vec{r’}= x’\hat i + y’ \hat j + z’ \hat k
\end{equation}
By triangle law of vector addition and from $\Delta OO’P$
\begin{equation}
\vec{OP}=\vec{OO’}+\vec{O’P}\\
\vec r=\vec{v}t+\vec{r}\\
\vec{r’}=\vec r – \vec{v} t
\end{equation}

(b) When both the coordinates do not coincide with each other

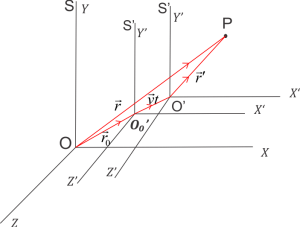
Let $\vec{r_0}$ be the position vector of the origin of refrance frame $S’$ whose origin initially is at $O’_0$ with respect to a constant frame of reference $S$ at $t=0$ and it is moving with a constant velocity $\vec v$ such that the axis od frame $S’$ is always parallel to the axis of frame $S$. At $t$ seconds $S’$ covers the distance $O’_0O’=\vec{v}t$. Now at this instant position vector of point $P$ would be $\vec{r’}$. Noe by triangle law of vector addition
\begin{equation}
\vec{OP}=\vec{O’_0 O’}+\vec{O’P}\\
\vec r = \vec{r_0}+\vec v t+\vec{r’} \\
\vec{r’}=(\vec r -\vec{r_0})-\vec v t
\end{equation}