This article is about Maxwell’s Equations.
1. Integral Form of Gauss’s Law
Under this heading, I’ll cover ” Gauss’s law for electric fields ” which is among one of Maxwell’s equations. In this article, I’ll try to cover the Integral form of Gauss’s Law.
Gauss’s law for electric fields as we all know deals with the electrostatic field, this law to be a powerful tool because it relates the spatial behavior of the electrostatic field to the charge distribution that produces it.
In the integral form, we write Gauss’s Law as
$ \oint\limits_s {\overrightarrow E \cdot \widehat nda = \frac{{{q_{enc}}}}{{{\varepsilon _0}}}} $
So main idea of Gauss’s law is
Electric charge produces an electric field, and the flux of that field passing through any closed surface is proportional to the total charge contained within that surface.
This is nothing but the statement of Gauss’s Law. So throughout this post, you will hang on to this main idea while I explain the meaning of each and every symbol used in the integral form of Gauss’s Law.
- Integral sign: Tells you to sum up the contributions from each portion of the surface
- Circle in integral sign: tells you that integral is taken over the closed surface
- $S$ in integral subscript: It mentions that integral is to be taken over a surface so the integral is not a volume or line integral.
- $ E$: It is the electric field measured in N/C. It represents the total electric field at each point on the surface under consideration. The surface may be real or imaginary.
- $\rightarrow $: above $E$ shows that the electric field is a vector quantity.
- $\cdot $: Dot product tells you to find the part of the electric field that is perpendicular to the surface. It stands for vector scalar product. In Gauss’s law, the circle between $\vec{E}$ and $\hat{n}$ represents the dot product (or ‘‘scalar product’’) between the electric field vector $\vec{E}$ and the unit normal vector $\hat{n}$ and the dot product between two vectors gives a scalar result.
- $\hat{n} $: It is the unit vector normal to the surface. The concept of the unit normal vector that at any point on a surface is simple, for this, imagine a vector with the length of one pointing in the direction perpendicular to the surface. It is called a ‘‘unit’’ vector because its length is unity and ‘‘normal’’ because it is perpendicular to the surface.
- $\vec{E}\cdot\hat{n} $: this expression represents the component of the electric field vector that is perpendicular to the surface under consideration. It is the projection of the first vector on the second vector multiplied by the length of the second vector. that is
$\vec{E}\cdot \hat{n}=|\vec{E}||\hat{n}|cos\theta =|\vec{E}|cos\theta $
where $\theta$ is the angle between unit normal $\hat{n}$ and $\vec{E}$
for $\theta=90^{0}$ , $|\vec{E}|cos\theta=0$ that is component of electric field perpendicular to the surface is zero.
For $\theta=0^{0}$ , $|\vec{E}|cos\theta=|\vec{E}|$ that is component of electric field perpendicular to the surface is the entire length of vector $\vec{E}$ . - $da$ : is the surface area in $m^{2}$
- $ q$: is the amount of charge in Coulomb.
- subscript $enc$ as in $q_{enc} $: Reminder that only the charge enclosed in the surface contributes to the integral.
- $\varepsilon_{0} $: is the electric permittivity of free space
Now there are two basic types of problems that you can solve using this equation
- The first case is where you have information about the distribution of electric charge and you want to find out the electric flux through the surface that encloses the charge
- In the second case you have information about the electric field through a closed surface and you want to find out the total charge enclosed by that surface.
Also, I am sure you know that the Gauss’s Law is highly symmetric and a powerful tool and you can use the law to find electric field itself rather than just finding the electric flux over a surface.
2. The differential form of Gauss’s Law For Electric Field
The integral form of Gauss’s law for electric fields relates the electric flux over a surface to the charge enclosed by that surface. Like all of Maxwell’s Equations, Gauss’s law may also be written in differential form. So, the Differential form of Gauss’s Law is
$\vec{\nabla }\cdot \vec{E}=\frac{\rho }{\epsilon _{0}}$
Now, the differential form of Gauss’s law tells us how field behaves at a point which integral form of Gauss’s law can not tell, but both these laws describe the same physical phenomenon. You can use any of the forms depending on how useful that form is to the problem you are trying to solve.
The left-hand side of the equation is the divergence of the electric field that is, the tendency of the field to ‘‘flow’’ away from a specified location, and the right side is the electric charge density divided by the permittivity of free space.
The main idea behind Gauss’s law in differential form is
The electric field produced by electric charge diverges from positive charge and converges upon negative charge.
Here we shall note that the only places at which the divergence of the electric field is not zero are those locations at which charge is present. So, if a positive charge is present then the divergence is positive which means that the electric field tends to ‘‘flow’’ away from that location. Now if negative charge is present then the divergence is negative and the field lines tend to ‘‘flow’’ toward that point.
The differential form of Gauss’s Law:- This form deals with the divergence of the electric field and the charge density at individual points in space.
The integral form of Gauss’s Law:- This form involves the integral of the normal component of the electric field over a surface.
If you know about spatial variation of the vector electric field is at a specified location then you can find the volume charge density at that location using this form. And if the volume charge density is known, then
the divergence of the electric field may be determined.
So now you know about the essential difference between both the forms (note:- The differential form and the integral form are the same thing) I shall go ahead and describe each and every symbol used in the mathematical form of this law.
- $\nabla $ the del operator:- Now I’ll try to explain what it is for in this law. Here the presence of this operator tells you that you have to take the derivative of the quantity (here $\vec{E}$) on which it is acting. Here it is used with a dot ($\vec{\nabla }\cdot \vec{E}$) which indicates you have to take the divergence of the physical quantity.
- The divergence ($\vec{\nabla }\cdot$) :- Now the concept of divergence is very important when it comes to be about studying physics and engineering where you bother yourself with the behavior of vector fields. Both flux and divergence deals with the flow of a vector field but there is an important difference that is flux is defined over an area, while divergence applies to individual points. Now consider the case of flowing fluid here the divergence at any point is a measure of the tendency of the flow vectors to diverge from that point (that is, to carry more material away from it than is brought toward it). Thus points of positive divergence are sources (faucets in situations involving fluid flow, positive electric charge in electrostatics), while points of negative divergence are sinks (drains in fluid flow, the negative charge in electrostatics).
- The divergence ($\vec{\nabla }\cdot \vec{E}$) of the electric field:- This expression represents the divergence of the electric field in Gauss’s Law. In electrostatics, as we already know all electric field lines begin on points of positive charge and terminate on points of negative charge, so it is obvious that this expression is proportional to the electric charge density at the location under consideration. So divergence at any point is simply not about spacing of field lines but it is about whether the flux out of an infinitesimally small volume around the point is greater than, equal to, or less than the flux into that volume. So if flux in the outward direction is greater than the inwards flux then the divergence is positive and if the inward flux is greater than the outwards flux then the divergence is negative at that point. Also if the outward and inward fluxes are equal the divergence is zero at that point.
- $ \rho$:- It is the charge density in coulombs per cubic meter
Now you know about the differential form of the Gauss’s Law and what makes it different from its integral form although conceptually both are same you can solve the problems related to this topic. You can even practice little mathematics where you can prove the equality of both the forms of Gauss’s Law.
3. The integral form of Gauss’s Law for magnetic fields
This is the second Maxwell’s equation which is about magnetic fields. So this article would be about the Integral form of Gauss’s Law for magnetic fields.
The integral form of Gauss’s Law for magnetic field is written as
$\oint\limits_S {\overrightarrow B \cdot \widehat nda} = 0$
Here in above equation left the side of is a mathematical description of the flux of a vector field through a closed surface. Here as you know Gauss’s law refers to the magnetic flux which is the number of magnetic field lines passing through a closed surface S. The right side of the equation is zero.
Gauss’s Law for magnetic field states that
The total magnetic flux passing through any closed surface is zero
Surface mentioned here can be real or imaginary and can be of any shape and size. Here it is mentioned that flux through any closed surface must be zero but this does not mean that magnetic field lies do not pass through the surface it means that when a magnetic field line enters the surface there must be a magnetic field line leaving the volume enclosed by the surface under consideration.
Gauss’s Law of magnetic field arises directly as a result of lack of existence of magnetic monopoles in nature. So isolated magnetic poles simply do not exist. Every magnetic north pole is accompanied by a magnetic south pole. Thus the right side of Gauss’s law for magnetic fields is identically zero.
Now I’ll give a brief explanation of the meaning of each and every symbol used in the Integral form of Gauss’s Law for magnetic field
- $\oint {} $ – Reminds that the integral is been taken over the closed surface
- $S$ – It reminds that it is a surface integral not a volume or line integral
- ${\overrightarrow B }$ The magnetic field – A magnetic field is the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude; as such it is a vector field (For more information visit this link ). Magnetic fields may be represented using field lines whose density in a plane perpendicular to the line direction is proportional to the strength of the field.
- $\oint\limits_S {\overrightarrow B \cdot \widehat nda} $ Magnetic Flux – Magnetic flux through any surface is is the amount of magnetic field flowing through the surface. Calculating this quantity depends on the situations like
- ${\varphi _B} = \left| {\overrightarrow B } \right| \times ({\text{surface area)}}$ when $ \overrightarrow B $ is uniform and perpendicular to the surface $S$
- ${\varphi _B} = \overrightarrow B \cdot \widehat n \times ({\text{surface area)}}$ when $ \overrightarrow B $ is uniform and at an angle to the surface $S$
- ${\varphi _B} = \int\limits_S {\overrightarrow B \cdot \widehat nda} $ when $ \overrightarrow B $ is nonuniform and at an variable angle to the surface $S$
Magnetic flux is a scalar quantity and the units of magnetic flux is ‘‘webers’’ abbreviated as $Wb$. The magnetic flux through a surface may be considered to be the number of magnetic field lines penetrating that surface and you must establish a relationship between the number of lines you draw and the strength of the field. When considering magnetic flux through a closed surface, it is important that you remember that surface penetration is taking both ways that is outward flux and inward flux have opposite signs.Thus equal amounts of outward (positive) flux and inward (negative) flux will cancel, producing zero net flux. The outward and inward magnetic flux must be equal and opposite through any closed surface. The number of field lines entering the volume enclosed by the surface is exactly equal to the number of field lines leaving that volume. This mean that the net magnetic flux through any closed surface must always be zero
So, the net magnetic flux passing through any closed surface must be zero because magnetic field lines always form complete loops.
4. The differential form of Gauss’s Law for Magnetic Field
Now this section is about the Differential form of Gauss’s Law for Magnetic Field
The differential form of Gauss’s Law for magnetic fields is written as
$\vec{\nabla} \cdot \vec{B}=0$
The left side of this equation is simply a mathematical description of the divergence of the magnetic field which is the tendency of the magnetic field to flow more strongly away from a point than toward it and the right side is simply zero. So Gauss’s Law in differential form states that
The divergence of magnetic field at any point is zero
Now in case of differential form of Gauss’s law for electric fields divergence of electric field is proportional to electric charge density but here in case of magnetic fields divergence of field at any point is zero because here it is not possible to have isolated magnetic poles as magnetic poles always appear in pair of north and south poles. So there is no such thing as magnetic charge density and this means that divergence of the magnetic field is zero.
Now I shall write about the meaning of each symbol used in the mathematical form of the differential form of Gauss’s law for magnetic fields
- $\vec{\nabla} $: $\nabla$ is the differential operator known as ‘del’ or ‘nabla’ operator and overhead arrow reminds that this del operator is a vector.
- $\cdot $: The dot product turns the del operator into the divergence.
- $\vec{B} $: $\vec{B}$ is the magnetic field measured in Tesla and it is a vector quantity.
- $\vec{\nabla} \cdot \vec{B}$ of the magnetic field: This expression gives the divergence of the magnetic field. Since divergence is by definition the tendency of a field to ‘‘flow’’ away from a point and since no point sources or sinks of the magnetic field are present so the amount of ‘‘incoming’’ field is exactly the same as the amount of ‘‘outgoing’’ field at every point. Vector fields with zero divergences are called ‘‘solenoidal’’ fields, and all magnetic fields are solenoidal.
5. The integral form of Faraday’s law
Now in this section, we would learn about the Integral form of Faraday’s law.
The integral form of Faraday Law is given by the following equation
\(\oint\limits_C {\overrightarrow E \cdot d\overrightarrow l } = – \int\limits_s {\frac{{\partial \overrightarrow B }}{{\partial t}} \cdot } \hat nda\)
The main idea of Faraday’s Law is
Changing magnetic flux through a surface induces an emf in any boundary path of that surface, and a changing magnetic field induces a circulating electric field.
So, if flux through any surface changes, an electric field is produced along the boundary of that surface. Again if there is a conducting material present along that boundary then induced field provides an emf that produces a current through that conducting material. Moving a bar magnet through a loop of wire produces an electric current in the wire but if you hold magnet stationary with respect to the loop there would be no induced current.
The negative sign in Faraday’s law tells you that the induced emf opposes the change in flux – that is, it tends to maintain the existing flux. This is called Lenz’s law.
Now I’ll try to explain the meaning of each and every symbol used in the integral form of Faraday’s law by first considering the left-hand side of the equation
- The integral on the left-hand side is a line integral along a closed path C it tells us to sum the contribution from each portion of closed path \(C\) . So integral is line integral not a surface integral.
- \(\overrightarrow E \) is the induced electric field in V/m and is a vector quantity. This electric field is produced by the changing magnetic fields and have field lines that loop back on themselves with no points of origin or termination and have zero divergences. The electric field appearing in Faraday Law is the field measured in the reference frame of each segment \({d\overrightarrow l }\) of the path over which the circulation is calculated and this distinction is made only because it is only in this frame that the electric field lines actually circulate back to themselves as can be seen in the figure given below
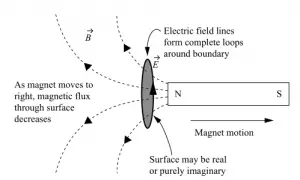
- Dot product tells you to find the part of \(\overrightarrow E \) parallel to \({d\overrightarrow l }\) (along path C)
- \({d\overrightarrow l }\) is an incremental segment of path \(C\)
- Right side as a whole is the flux of the time rate of the change of the magnetic field.
- \({\frac{{\partial \overrightarrow B }}{{\partial t}}}\) is the rate of change of magnetic field with time.
We can use Faraday’s law and the flux rule in solving a variety of problems that have changing magnetic flux and induced electric fields, in particular, problems of two types:
(1) Given information about the changing magnetic flux, find the induced emf.
(2) Given the induced emf on a specified path, determine the rate of change of the magnetic field magnitude or direction or the area bounded by the path.
In situations of high symmetry, in addition to finding the induced emf, it is also possible to find the induced electric field when the rate of change of the magnetic field is known.
6. The differential form of Faraday’s law
Faraday’s Law in differential form is written as
\(\overrightarrow \nabla \times \overrightarrow E = – \frac{{\partial \vec B}}{{\partial t}}\)
From the left side of the equation is nothing but the curl of the electric field and it tells about the tendency of field lines to circulate around a point . Curl of a vector means how much the vector curls around the point in question. The right side represents the rate of change of magnetic field with time. So from this it could be stated that
A circulating electric field is produced by a magnetic field that changes with time.
Now I’ll try to explain the meaning of each and every symbol used in integral form of Faraday’s law by first considering the left hand side of the equation
- \(\vec \nabla \times \vec E\) : here \(\vec \nabla\) is a differential vector operator and the cross product turns the del operator into the curl and \( \vec E \) is electric field measured in V/m. The curl of a vector field is a measure of the field’s tendency to circulate about a point – much like the divergence is a measure of the tendency of the field to flow away from a point. Now when we talk about point charges electric fields diverge away from points of positive charge and converge toward points of negative charge, such fields cannot circulate back on themselves. So what kind of fields circulates back on themselves? Electric fields induced by changing magnetic fields are different. Wherever a changing magnetic field exists, a circulating electric field is induced. Unlike charge-based electric fields, induced fields have no origination or termination points – they are
continuous and circulate back on themselves. - $\frac{\partial B }{\partial t} $: is the rate of change of the magnetic field with time.
NOTE:- Two equations are left and I’ll update the article soon.
