Ferromagnetism

• A ferromagnetic material has a spontaneous magnetic moment- magnetic moment even in zero applied magnetic field this means that electron spins and magnetic moments are arranged in a regular manner.
• Consider a paramagnet with a concentration of N ions of spin S. Given an internal interaction tending to line up the magnetic moments parallel to each other, we shall have a ferromagnet.
• This internal interaction is called an exchange field.
• Orienting effect of the exchange field is opposed by thermal agitation.
• At elevated temperatures, the spin order is destroyed.
• Exchange field can be treated as equivalent to BE (magnetic field) also assume that the exchange field B_E is proportional to the magnetization M.
• Magnetization M is defined as the magnetic moment per unit volume.
• In mean-field approximation, each magnetic atom experiences a field proportional to the magnetizationB_E=λM (1)
  Where λ is constant independent of temperature.
• Each spin sees average magnetization of all the other spins and more precisely of the neighboring spins.
• Curie Temperature (T_c) is the temperature above which spontaneous magnetization vanishes.
• T_c separates disordered paramagnetic phase at temperature T > T_c from ordered ferromagnetic phase at temperature T < T_c.
• If B_a is the external magnetic field then the effective field acting on atom or ion isB= B_a+ B_E = B_a+ λM
• If χ_p is paramagnetic susceptibility then
  M= χ_p( B_a+ B_E)
  χ_p=C/T from curie law for paramagnetic materials
  this implies that MT=C(B_a+ λM)
• Susceptibility has a singularity at T=Cλ.
• At this temperature and below there exists a spontaneous magnetization because if χ is infinite, we can have a finite M for zero B_a.
• Curie-Weiss law is
  χ=C/(T-T_c) or T_c=Cλ
• This spontaneous magnetization decreases very slowly as the temperature is first raised above absolute zero and drops more steeply at higher temperatures until finally falls to zero at Curie temperature.

Nature of Ferromagnetic carriers

• Entire magnetization must be essentially associated with electron spin, and not at all with the orbital motion of electrons.
• Argon core (1s²2s²2p⁶3s²3p⁶) of Fe, Co and Ni can be left out of account as a source of ferromagnetism.
• 4s electrons are responsible for electrical conductivity and crystal binding.
• Thus 3d electrons with unpaired spins are responsible for magnetization of these metals.
• An effective number of magnetic moment carriers per atom should be non-integral, despite that each atom has an integral number of electrons Fe – 4 electrons: Co – 3 electrons: Ni – 2 electrons and each electron contributes a magnetic moment of 1μ_B due to spin alone.
• Above argument applies to a free atom but here they are bound into solids where atomic levels are bounded into bands.
• Non-integral values 2.22μ_B, 1.72μ_B, and 0.54μ_B for Fe, Co, and Ni respectively. of magnetic moment carriers which each atom supplies can be explained as follows: Wide 4s band of these metals overlaps with a narrow 3d band. As a consequence, there is, on an average a certain fraction of total number of 3d plus 4s electrons in each band; the relative occupation of two bands being determined by Fermi level E_F

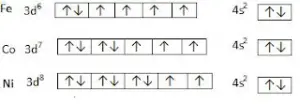
for example, in case of nickel 10 sd electrons are distributed in them in such a way that on the average 9.40 electrons are in 3d band and 0.6 in a 4s band. In accordance with Hund rule, 5 electrons set their spins parallel to the field and remaining 4.40 set their spins antiparallel to the field. Thus net parallel spin of Ni atom would be 5-4.40 = 0.60 and hence magnetic moment is 0.60μ_B agrees fairly with the experimental value

Origin of exchange interaction

• Explanation of large value of the molecular field is based on non-magnetic interaction that is exchanged interaction.
• Exchange interaction arises as a consequence of Pauli’s Exclusion principle. Because of this principle, we can not change the relative orientation of two spins without changing the spatial distribution of charge, clearly indicating that interaction exists between two atoms.
• This interaction depends on the relative orientation of electron spins not on the magnetic moments.
• The energy of this interaction between atoms i, j bearing spins S_i , S_j is of the form E_ex=-2J_eS_i.S_j where J_e is the exchange integral, its value is related to the overlap of the charge distribution of atoms i and j i.e., on their interatomic separation.
• The energy of a parallel configuration is lower than that of anti-parallel by amount 2J_e this implies that former configuration is more stable favoring magnetization to occur.
• Note that exchange interaction is positive only for iron group and negative for others.

Ferromagnetic domains

• The fundamental problem of ferromagnetism is to explain why the elementary moments of ferromagnetic material can be aligned so much more easily than those of paramagnetic materials.
• Weiss suggested that these were forces of interaction between elementary magnetic moments tending to make each one parallel to their neighbors.
• Such forces would cause all moments to be aligned in the same direction at absolute zero of temperature and this ordering of moments would continue when the temperature is raised, though with increasing deviation from perfect alignment, until a critical temperature is reached, above which the moments are arranged in random, as in a paramagnetic material.
• Weiss theory can thus account for the fact that ferromagnetic materials may be spontaneously magnetized even in the absence of an external magnetic field; it does not explain why the majority of ferromagnetic are not actually found in this spontaneously magnetized state but are much more likely to have zero magnetization.
• This difficulty can be met by introducing the hypothesis of domain theory.
• Here supposed that the forces of interaction only maintained the parallel alignment of elementary moments over fairly small regions.
• Actual specimen is composed of small regions called domains, within each of which the local magnetization is saturated.
• The direction of magnetization of different domains need not be parallel.
• The increase of gross magnetic moment of a ferromagnetic specimen in an applied magnetic field takes place by two independent processes : (1) In weak applied fields the volume of domains favorably oriented w.r.t. the field increases at the expense of unfavorably oriented domains         (2) In strong applied fields the domain magnetization rotates towards the direction of the field.