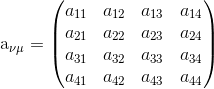Derivation of Lorentz transformation equations using orthogonal transformations
Let us consider two uniformly moving frames of reference where origins coincides at $t=0$. let the source of light is fixed at unprimed frame of reference and emits a pulse of light. The observer fixed in the unprimed frame of reference will observe a spherical wave-front propagating with the speed of light $c$ , whose equation can be written as
$x^2+y^2+z^2 = c^2 t^2$ (1)
Since speed of light is invariant according to special theory of relativity so the observer fixed in the primed frame of reference would also observe the light pulse propagating as the spherical wave-front from his own origin whose equation is
$x’^2+y’^2+’z^2 = c^2 t’^2$ (2)
We now need appropriate transformation equations because here we note that time is no more scalar invariant. The transformations should be such that the light pulse viewed from both the frames of reference must be in form that wave pulse is propagating as simultaneously concentric spheres in both the systems. This reveals that
$ x^2+y^2+z^2 – c^2 t^2 = x’^2+y’^2+’z^2 = c^2 t’^2 $ (3)
or in terms of $x_1$,$x_2$,$x_3$ and $x_4$ where $x_4=ict$ we have
$x_1^2 + x_2^2 + x_3^2 + x_4^2 = x’_1^2 + x’_2^2 + x’_3^2 + x’_4^2$
or,
$\sum\limits_{\mu = 1}^4 {x_\mu ^2} = \sum\limits_{\mu = 1}^4 {x’_\mu ^2} $ (4)
Thus square of radius vector is invariant under a transformation of co-ordinates in four dimensional space. We can thus say that equation (4) represents the orthogonal transformation of vectors in four dimensional Minkowiski space. Thus Lorentz transformations can be represented as
$x{‘_\mu } = \sum\limits_{\mu = 1}^4 {{a_{\nu \mu }}{x_\nu }} $
where
is a linear transformation matrix. Now here frame $S’$ is moving w.r.t. $S$ with velocity $v$ in the positive $x_3$ direction and all the axis of $S’$ are parallel to that of $S$. We will now obtain the matrix element $a_{\mu\nu}$ of transformation between $x$ and $x’$ for pure Lorentz transformation.
$x{‘_\mu } = \sum\limits_{\mu = 1}^4 {{a_{\nu \mu }}{x_\nu }} $ (5)
or,

or
$x’_{1}=a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}+a_{14}x_{4}$
$x’_{2}=a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}+a_{24}x_{4}$
$x’_{3}=a_{31}x_{1}+a_{32}x_{2}+a_{33}x_{3}+a_{34}x_{4}$
$x’_{4}=a_{41}x_{1}+a_{42}x_{2}+a_{43}x_{3}+a_{44}x_{4}$ (equations 6)
As the primed system is taken to be moving along $x_3$ axis , then $x_1$ and $x_2$, being in a direction perpendicular to that system , motion will remain unaffected by the transformation i.e.,
$x’_{1}=x_{1}$
$x’_{2}=x_{2}$
as the components $x_3$ and $x_4$ are the components to undergo transformation so components $x_1$ and $x_2$ should not appear in the transformation matrix of $x’_3$ and $x’_4$. Thus above equation 6 becomes
$x’_{1}=x_{1}$
$x’_{2}=x_{2}$
$x’_{3}=a_{33}x_{3}+a_{34}x_{4}$
$x’_{4}=a_{43}x_{3}+a_{44}x_{4}$ (equations 7)
Therefore the transformation matrix is
$\begin{pmatrix}
1 &0 &0 &0 \\
0& 1 & 0 &0 \\
0& 0 &a_{33} &a_{34} \\
0 & 0 & a_{43} &a_{44}
\end{pmatrix}$ (8)
Further since these matrix elements must obey the orthogonality condition that is,
$\sum_{\nu}a_{\mu \nu}a_{\lambda\nu}=\delta_{\mu\nu}$ (9)
it is $=1$ if $\mu=\lambda$ and it is $=0$ if $\mu\neq \lambda$
putting $\mu=\lambda=3$ , and first $\nu=3$ and second $\nu=4$ we get
$a_{33}^{2}+a_{34}^{2}=1$ (10)
Also with $\mu=\lambda=4$, $\nu=3$ and $\nu=4$ we get
$a_{43}^{2}+a_{44}^{2}=1$ (11)
$a_{33}a_{43}+a_{34}a_{44}=0$ (12)
Thus the orthogonality condition furnishes the above three equations connecting the four matrix elements.
The four unknown elements can be determined uniquely when the fourth relation between them is provided. We know that the origin of primed frame is $(x’_{3}=0)$ is moving uniformly along $x_3$ axis; thus after time $t$ it’s $x_3$ co-ordinate will be $vt$, i.e.,
$x_3=vt=v\frac{x_4}{ic}=-\frac{iv}{c}x_4=-i\beta x_4$
which, with matrix relation for $x’_3$ gives
$x’_{3} = a_{33} x_{3} +a_{34} x_{4}$
$x’_{3}=(a_{34}-i\beta a_{33})x_{4}=0$
$a_{34}=i\beta a_{33}$
which when substituted with equation 10 gives
$a_{33}=\frac{1}{\sqrt{1-\beta^2}}$
so that,
$a_{34}=\frac{i\beta}{\sqrt{1-\beta^2}}$
On solving equation 11 and equation 12 it is quite easy to show that
$a_{44}=\frac{1}{\sqrt{1-\beta^2}}$ and $a_{43}=-\frac{i\beta}{\sqrt{1-\beta^2}}$
We can now write the Lorentz transformation as
$\begin{pmatrix}
x’_1\\
x’_2\\
x’_3\\
x’_4
\end{pmatrix}=\begin{pmatrix}
1 &0 &0 &0 \\
0 & 1& 0 &0 \\
0 & 0 & \frac{1}{\sqrt{1-\beta^2}} &\frac{i\beta}{\sqrt{1-\beta^2}} \\
0& 0 & -\frac{i\beta}{\sqrt{1-\beta^2}} & \frac{1}{\sqrt{1-\beta^2}}
\end{pmatrix}\begin{pmatrix}
x_1\\
x_2\\
x_3\\
x_4
\end{pmatrix}$
or,
$ \begin{pmatrix}
x’_1\\
x’_2\\
x’_3\\
ict’
\end{pmatrix}=\begin{pmatrix}
1 &0 &0 &0 \\
0 & 1& 0 &0 \\
0 & 0 & \frac{1}{\sqrt{1-\beta^2}} &\frac{i\beta}{\sqrt{1-\beta^2}} \\
0& 0 & -\frac{i\beta}{\sqrt{1-\beta^2}} & \frac{1}{\sqrt{1-\beta^2}}
\end{pmatrix}\begin{pmatrix}
x_1\\
x_2\\
x_3\\
ict
\end{pmatrix} $
giving
$x’=x\\
y’=y\\
z’=\frac{z-vt}{\sqrt{1-\beta^2}}\\
ict’=z\left ( -\frac{i\beta}{\sqrt{1-\beta^2}} \right ) +\frac{ict}{\sqrt{1-\beta^2}}$ (13)
or,
$t’=\frac{t-\left ( \frac{v}{c^2} \right )z}{\sqrt{1-\beta^2}}$
equations 13 are known as Lorentz transformation equations. Lorentz transformation to real co-ordinate is possible when $\beta<1$ indicating that one can not have relative velocity greater than $c$, the sped of light.