Brachistochrone Problem

Brachistochrone Problem Solution

Brachistochrone Problem :
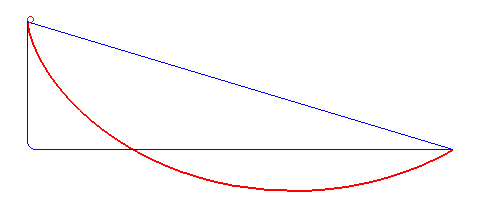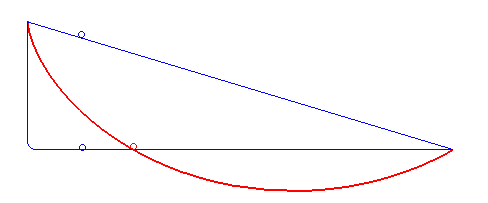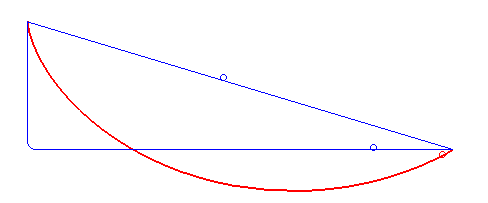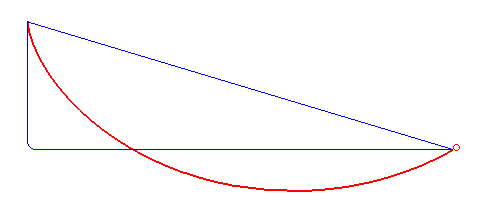
If a particle falls from rest under the influence of gravity from a higher to lower point in the minimum time, what is the curve that the particle will follow?

Solution

Suppose $v$ is the speed of the particle along the curve, then in traversing ds portion of the curve time spent would be \(\frac{{ds}}{v}\) so that total time taken by the particle in moving from highest point 1 to lowest point 2 will be

\({t_{12}} = \int\limits_1^2 {\frac{{ds}}{v}} \)

Suppose vertical distance of fall upto point 2 be x, then from the principle of conservation of energy of the particle we find that
\[\begin{array}{*{20}{l}}
{\frac{1}{2}m{v^2} = mgx}\\
{or}\\
{v = \sqrt {2gx} }\\
{then}\\
{{t_{12}} = \int\limits_1^2 {\frac{{\sqrt {d{x^2} + d{y^2}} }}{{\sqrt {2gx} }}} dx}\\
{{\rm{ = }}\int\limits_1^2 {\frac{{\sqrt {1 + {{\dot y}^2}} }}{{\sqrt {2gx} }}} dx}\\
{{\rm{ = }}\int\limits_1^2 {fdx} }
\end{array}\]

Where,

\( f=\left ( \frac{1+\dot{y}^{2}}{2gx} \right )^{\frac{1}{2}} \)

For \({t_{12}}\) to be minimum equation

\(\frac{d}{{dx}}\left( {\frac{{\partial f}}{{\partial \dot y}}} \right) – \frac{{\partial f}}{{\partial y}} = 0\)

must be satisfied. From expression for \(f\) we find that

\(\begin{array}{l}\frac{{\partial f}}{{\partial y}} = 0\\\frac{{\partial f}}{{\partial \dot y}} = \frac{{\dot y}}{{\sqrt {2gx} \sqrt {1 + {{\dot y}^2}} }}\\\frac{d}{{dx}}\left( {\frac{{\dot y}}{{\sqrt {2gx} \sqrt {1 + {{\dot y}^2}} }}} \right) = 0\\or\\\frac{{{{\dot y}^2}}}{{2gx(1 + {{\dot y}^2})}} = c’\end{array}\)

Where c’ is the constant of integration.
Since c’ is a constant we can also write

\(\frac{{{{\dot y}^2}}}{{x(1 + {{\dot y}^2})}} = c\)

where c is also a constant. On integrating above equation we find

\(\begin{array}{l}\frac{{{{\dot y}^2}}}{c} = x(1 + {{\dot y}^2})\\or,\\{{\dot y}^2}\left( {\frac{1}{c} – x} \right) = x\\{{\dot y}^2}\left( {\frac{x}{c} – {x^2}} \right) = {x^2}\\\dot y = \frac{x}{{\sqrt {\frac{x}{c} – {x^2}} }}\end{array}\)

Putting \(\frac{1}{c} = 2a\) , and on integration we get

\(\int dy=\int \frac{x}{\sqrt{2ax-x^{2}}}dx\)

\( y=acos^{-1}(1-\frac{x}{a})-(2ax-x^{2})^{1/2}+c”\)

where c” is new constant of integration.
In case c” is zero then y will be zero for x=0.
As such the equation

\( y=acos^{-1}(1-\frac{x}{a})-(2ax-x^{2})^{1/2}\)

And this y represents an inverted cycloid with its base along y-axis and cusp at the origin and is the curve that particle will follow.