This article is about the revision of Particle properties of wave. I’ll be doing detailed articles on each one of the sub-topics given in this article.
- Classical Mechanics do not put any restriction on values of a dynamical property of a particle, so small and large both values are permitted.
- Principle of superposition:- When two or more waves of the same nature travel past the same point at the same time, the instantaneous amplitude of the resultant wave is the sum of the instantaneous amplitudes of the individual waves.
- In Electromagnetic waves magnitude of $E$ is used as instantaneous amplitude, since it is electric field of light waves whose interactions with matter give rise to normally all common optical effects.
1. Black Body Radiation
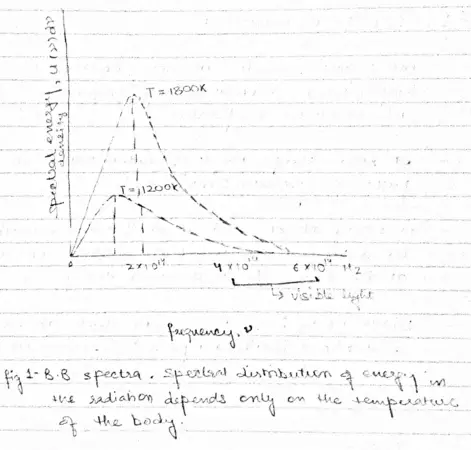
- All objects radiate EM energy continuously irrespective of their temperatures, though which frequency predominates depends on the temperature.
- At room temperature most of radiations are in infra red part of the spectrum which is invisible.
- A body at constant $T$ is in thermal equilibrium with its surroundings and must absorb energy from them at same rate as it emits energy.
- Black Body:- Ideal body that absorbs all radiations incident upon it regardless of frequency.
- Approximate Ideal black body :- hollow object with very small hole leading to its interior.
- Radiation strike the hole $\rightarrow $ enters the cavity $\rightarrow $ it is trapped by reflection back and forth till it is absorbed.
- Cavity walls are continuously emitting and absorbing radiations.
- A black body radiates more when it is hot then when it is cold.
- Spectrum of hot black body has its peak at a higher frequency then the peak in the spectrum of a cooler one as shown below in the figure
Ultraviolet catastrophe
- Why does the Black body spectrum has the shape as shown in the above figure. This problem was examined by Rayleigh and James Jeans.
- They consider the radiation inside cavity of absolute temperature $T$ to be a series of standing EM waves.
- Condition for standing wave in the cavity is such that the path length from wall to wall must be a whole number of half wavelengths, so that nodes occur at each reflecting surface.
- The number of standing waves $G(\nu)d\nu$
\begin{equation} \label{eq:poly}
g(\nu )d\nu = {{8\pi {\nu ^2}d\nu } \over {{c^3}}}
\end{equation}
above equation gives the density of standing waves in the cavity. Here you can see that this formula is independent of the shape of the cavity. Form this formula we can conclude that higher is the frequency, shorter the wavelength and greater would be the number of possible standing waves.
Theorem of equipartition of energy
Theorem of equipartition of energy states that average energy per degree of freedom of an entity (for example molecule of ideal gas) that is a member of a system of such entities in thermal equilibrium at temperature $T$ is $\frac{1}{2} kT$ , where $k=1.381 \times 10^{-23} \frac{J}{K}$
note:- degree of freedom is a mode of energy possession.
Each standing wave in a cavity originates in an oscillating electric charge in the cavity wall, two degrees of freedom are associated with the wave and it should have an average energy of $2\left ( \frac{1}{2} \right )kT$. So, Classical average energy per standing wave is
\begin{equation}
\bar{\epsilon}=kT
\end{equation}
Therefore total energy $u(\nu)d\nu$ per unit volume in the cavity in the frequency interval from $\nu$ to $\nu+d\nu$ is
\begin{equation}
u(\nu)d\nu=\bar{\epsilon}G(\nu)d\nu=\frac{8\pi kT}{c^{3}}\nu^{3}d\nu
\end{equation}
Above equation is called Rayleigh-Jeans formulae. Here we see that radiation rate is proportional to this energy density for frequencies between $\nu$ and $\nu+d\nu$
This formula predicts that as frequency $\nu$ increases towards the UV end of spectrum, energy density should increase a $\nu^{2}$. This implies that as $\nu\rightarrow \infty $ , $u(\nu)d(\nu) \rightarrow \infty $ but in reality energy density should fall to zero as $\nu\rightarrow \infty $
This discrepancy came to known as UV catastrophe of classical physics
Plank’s Radiation formulae
Plank’s formulae for spectral energy density of black body radiation is
\begin{equation}
u(\nu )d\nu = {{8\pi h} \over {{c^3}}} {{{\nu ^3}d\nu } \over e^{h\nu /kT}-1}
\end{equation}
where $h=6.626 \times 10^{-34}Js$ is the Plank’s constant
Now at high frequency $h\nu \ll kT$ this implies that $\frac{h\nu}{kT} \ll 1$ or in general
$$e^{x}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+……$$
This implies that for small x, $e^{x} \simeq 1+x$ this implies that $\frac{h\nu}{kT} \ll 1$
$$\frac{1}{e^{\frac{h\nu}{kT}}-1}\sim \frac{1}{1+\frac{h\nu}{kT}-1} \simeq \frac{kT}{h\nu}$$
Thus at low frequencies Plank’s formula becomes
$$u(\nu)d\nu\simeq\frac{8\pi ch}{c^{3}}\nu^{3}\left ( \frac{kT}{h\nu} \right )d\nu \simeq \frac{8\pi kT}{c^{3}}\nu^{2}d\nu$$
which is Rayleigh-Jeans formula
Justification of Plank’s formula
- The oscillators in the cavity walls could not have a continuous distribution of possible energies $\epsilon$ but must have only specific energies.
So, Oscillator energies
\begin{equation}
$\epsilon_{n}=nh\nu$
\end{equation}
where n=0,1,2,… - An oscillator emits radiation of frequency $\nu$ when it drops from one energy state to next lower one.
- It jumps to the next higher state when it absorbs radiation of frequency $\nu$.
- Each discrete bundle of energy $h\nu$ is called a quantum
- With oscillator energies limited to $nh\nu$ , actual energy per standing wave ould be
\begin{equation}
\epsilon=\frac{h\nu}{e^{\frac{h\nu}{kT}}-1}
\end{equation}
So the concept that the oscillators in cavity walls can interchange energy with standing waves in the cavity only in quanta $h\nu$ , is impossible to understand from point of view of classical physics.
2. X-Rays
- Consists of high energy photons
- A highly penetrating radiations of unknown nature was produced when fast electrons strike on matter.
- These radiations come to be known as X-Rays
- X-Rays travel in straight line
- are unaffected by electric and magnetic fields
- passes readily through opaque materials
- causes phosphorescent substances to glow
- exposes photographic plates
- Faster the original electrons, the more penetrating the resulting X-Rays and greater the number of electrons, the greater the intensity of X-Ray beams
- X-Rays are EM waves
- EM radiation with wavelengths from about 0.01 to about 10 nm falls into the catagory of X-Rays
- The X-Rays produced at given accelerating potential $V$ vary in wavelength, but none has a wavelength shorter than a certain value $\lambda_{min}$
- Increasing the value of $V$ decreases $\lambda_{min}$
$$\lambda_{min}=\frac{1.24 \times 10^{-6}}{V}Vm$$
X-Ray production is inverse of photoelectric effect.
Photoelectric Effect
- When radiation of high frequency is incident on a metal surface, electrons are emitted from the surface of the metal. These electrons are called photoelectrons and this phenomenon is called photoelectric effect
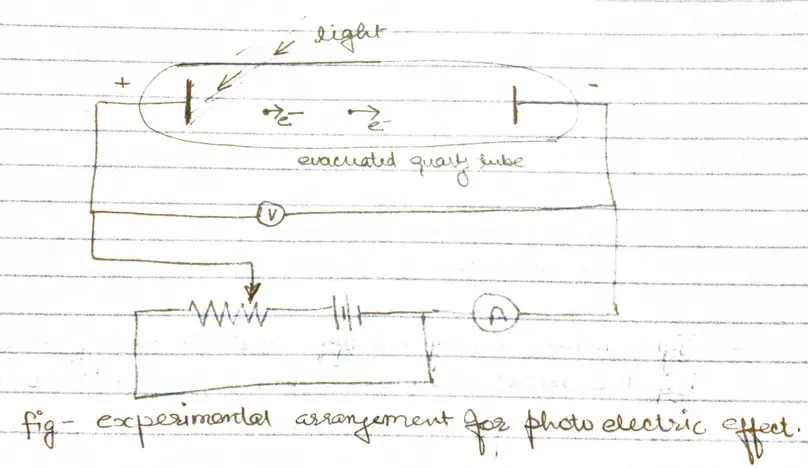
- Some of photoelectrons that emerge from anode surface have enough energy to reach the cathode despite of negative parity and constitute the measured current.
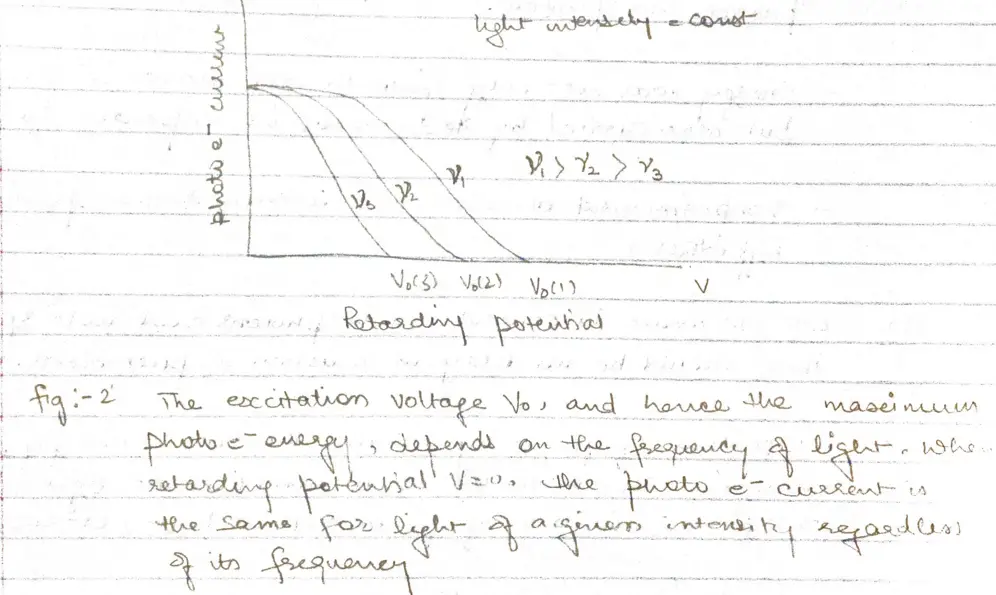
- When the voltage of the order of several volts is increased to a certain value $V_{0}$ , no more photoelectrons arrive, as indicated by current dropping to zero.
- This excitation voltage corresponds to the maximum photo electron kinetic energy
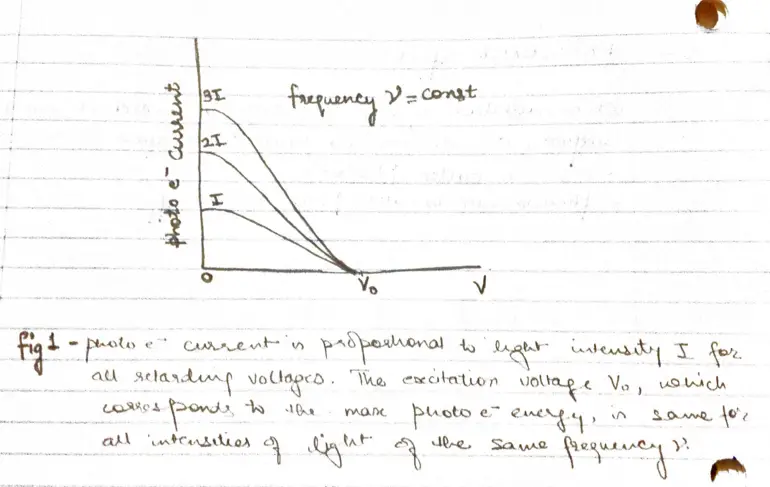
- But three experimental findings disagree above explanation
- Within experimental accuracy $(\sim 10^{-9}s)$, there is no time limit between the arrival of light at metal surface and the emission of photoelectrons
- A bright light yields more photoelectrons then a dim one of same frequency, but the electron energies remains the same.
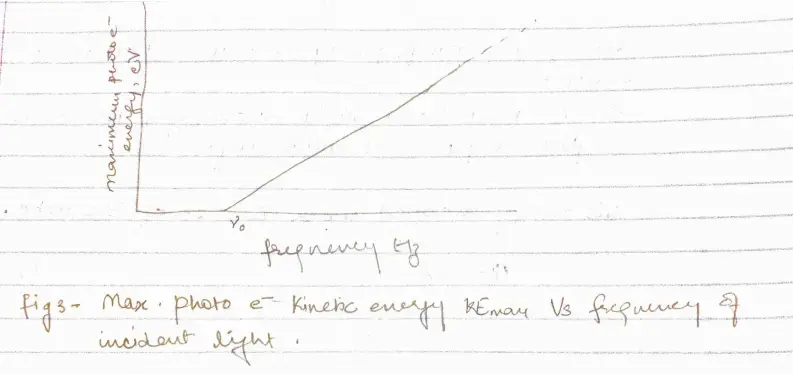
- Higher the frequency of light more energy the photoelectrons have (fig 2)
a. At frequency below a certain critical frequency $\nu_{0}$, which is characteristic of each particular metal, no electrons are emitted.
b. Above $\nu_{0}$ the photoelectrons range in energy from 0 to a maximum value that increases linearly with increasing frequency
Quantum theory of light
- Photoelectric effect could be understood if the energy in light is not spread out over wavefront but is concentrated in small packets or photons.
- Energy was not only given to EM waves in separate quanta but it is also carried by waves in separate quanta.
- Experimental observations directly follow this hypothesis
- Because EM waves is concentrated in photons and not spread out, there should be no delay in emission of photoelectrons.
- All photons of frequency $\nu$ have same energy, so changing the intensity of a monochromatic light beam will change the number of photoelectrons but not their energies
- Higher the frequency $\nu$, the greater the photon energy $h\nu$ and so the more energy the photoelectrons have.
- There is a critical frequency $\nu_{0}$ below which no photoelectrons are emitted. So, there must be a minimum energy $\phi$ for an electron to escape from a particular metal surface.
- This energy is called work function of the metal, and is
\begin{equation}
\phi=h\nu_{0}
\end{equation} - Greater the work function of the metal, more energy is needed for an electron to leave its surface, and higher would be the critical frequency for photoelectric emission to occur.
- Photoelectric effect in a given metal should obey the equation
\begin{equation}
h\nu = KE_{max}+\phi
\end{equation}
here,
$h\nu$ is the energy of photons
$ KE_{max}$ is the maximum photoelectron energy
$\phi$ is work function $\phi = h\nu_{0}$
this implies that $h\nu = KE_{max}+h\nu_{0}$ or,
\begin{equation}
KE_{max}=h(\nu-\nu_{0})
\end{equation}
If the energy $h\nu_{0}$ is needed to remove electrons from a metal surface, the maximum KE will be $h\nu – h\nu_{0}$ when lighy of frequency $\nu$ is directed at the surface.