Spherical coordinates system (Spherical polar coordinates)

 

The spherical polar coordinates represent the coordinates of points on the surface of a sphere in a covariant form. The coordinates of the point $P$ in this system is represented by the radial vector $r$ which is the distance from the origin to the point, the polar or zenith angle $\theta$ which is the angle the radial vector makes with respect to the z-axis and the azimuth or longitudinal angle $\phi$ which is which is the normal polar coordinate in the x − y plane as shown below in the figure.These co-ordinates are related to the rectangular coordinates x, y, and z through
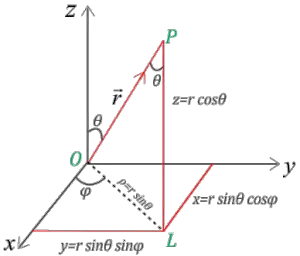
\begin{align}
x&=r\sin \theta \cos\varphi \\
y&=r\sin \theta \sin \varphi \\
z&=r\cos \theta
\end{align}
Spherical polar coordinates in terms of Cartesian coordinates are
\begin{align}
r&=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}} \\
\tan \theta &=\frac{\sqrt{{{x}^{2}}+{{y}^{2}}}}{z} \\
\tan \varphi & =\frac{y}{z}
\end{align}

 

 

Solved Problems on Spherical Polar co-ordinates

Question 1
How to Find Kinetic energy in terms of \((r,\theta ,\phi )\)
Solution 1
We have to find the kinetic energy in terms of \((r,\theta ,\phi )\) that is in terms of spherical c0-ordinates. Kinetic energy in terms of Cartesian co-ordinates is
\(T = \frac{1}{2}m\left( {{{\dot x}^2} + {{\dot y}^2} + {{\dot z}^2}} \right)\) (1)
Where \(\dot x,\dot y{\rm{ and }}\dot z\) are derivatives of z, y and z with respect to time.
Cartesian co-ordinates x, y, z in terms of \(r,\theta \) and \(\phi \) are
\(\begin{array}{l}x = r\sin \theta \cos \phi \\y = r\sin \theta \sin \phi \\z = r\cos \theta \end{array}\)
Now derivatives of x, y and z w.r.t. $t$ is
\(\begin{array}{l}\dot x = \frac{{dx}}{{dt}} = \dot r\sin \theta \cos \phi + r\cos \theta \cos \phi \dot \theta – r\sin \theta \sin \phi \dot \phi \\\dot y = \frac{{dy}}{{dt}} = \dot r\sin \theta \sin \phi + r\cos \theta \sin \phi \dot \theta + r\sin \theta \cos \phi \dot \phi \\\dot z = \frac{{dz}}{{dt}} = \dot r\cos \theta – r\sin \theta \dot \theta \end{array}\)
Where
\(\dot r = \frac{{dr}}{{dt}},\dot \theta = \frac{{d\theta }}{{dt}},\dot \phi = \frac{{d\phi }}{{dt}}\)
means all \(r,\theta \) and \(\phi \) changes with time as the particle moves or changes its position with time.
Now calculate for
\({\dot x^2},{\dot y^2},{\dot z^2}\)
and add them. After adding them we get
\({(\dot x)^2} + {(\dot y)^2} + {(\dot z)^2} = {\dot r^2} + {r^2}{\dot \theta ^2} + {r^2}{\sin ^2}\theta {\dot \phi ^2}\)
Putting this value of \({(\dot x)^2} + {(\dot y)^2} + {(\dot z)^2}\)in equation 1 we get kinetic energy of particle or system in terms of \(r,\theta \) and \(\phi \).
Hence,
\(T = \frac{1}{2}m({\dot r^2} + {r^2}{\dot \theta ^2} + {r^2}{\sin ^2}\theta {\dot \phi ^2})\)

Definitely, there is much much more information to be added to this topic. I’ll do it some other time.