Coulomb's law : statement , formula , questions and answers

Coulomb's Law statement

In 1785 the French physicist Charles Augustin Coulomb measured the electric force between small charged spheres using a torsion balance. He then formulated his observations in the form of Coulomb's Law. Coulomb's Law is an electrical analog of Newton's Universal Law of Gravitation. It states that

The force of attraction or repulsion between two stationary point charges is
(i) directly proportional to the product of the magnitude of two charges.
(ii) inversely proportional to the square of the distance between them.
This force acts along the line joining the two charges.

To explain above statement consider the figure given below

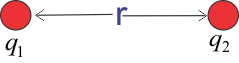
Above figure consists of two point charges $q_1$ and $q_2$. These two charges are separated by a distance $r$. Then according to Coulomb's Law the force $F$ of attraction or repulsion between them is,
$F \propto {q_1}{q_2}$ and $F \propto \frac{1}{r^2}$
Therefore,
$$F \propto \frac{q_{1}q_{2}}{r^{2}}\tag{1}$$
or,
$$F = k\frac{{{q_1}{q_2}}}{{{r^2}}}$$

where, $k$ is the constant of proportionality. The value of $k$ depends on the nature of the medium between two charges and the system of units we choose to measure $F$, $q_1$, $q_2$ and $r$.

In SI units system, when two charges are in vacuum or air

$$k = \frac{1}{4\pi \varepsilon_{0}}$$

where $\varepsilon_{0}$ is absolute permittivity of free space. Value of this constant in vacuum is $8.85 \times 10^{-12}C^2/Nm^2$. If we put the value of $\varepsilon_{0}$ in above equation for $k$ we find

$k= \frac{1}{4\pi \varepsilon_{0}} =\frac{1}{4 \times \pi \times 8.85 \times 10^{-12}C^2/Nm^2 } = 9 \times 10^{9} Nm^2C^{-2}$

So, from above equation (1) the force between two charges located in air or vacuum is given by,

$F = \frac{1}{4\pi \varepsilon_{0}} \frac{{{q_1}{q_2}}}{{{r^2}}}= 9 \times 10^{9} \times \frac{{{q_1}{q_2}}}{{{r^2}}} $ (in Newton)

Now if the charges are in a medium (glass, water etc.) other then air and vacuum then electric force between these two charges is

$$F = \frac{1}{4\pi \varepsilon} \frac{{{q_1}{q_2}}}{{{r^2}}}$$

where, $\varepsilon $ is a constant and is the the permittivity of the medium in which charges are present. Since the value of $\varepsilon $ depends on the medium, the magnitude of force on a charge also depends on the medium.

NOTE:-

1. The direction of the force is along the line joining two charges. It can be inward or outward depending on attraction or repulsion between the charges.
2. Coulomb's Law of electrostatics holds for two or more point charges ate rest.
3. SI unit of permittivity is $ C^2/Nm^2 $. It can also be expressed as farad per meter (F/m).

Unit of electric charge

Learn more about electric charge

SI unit of charge is Coulomb. We know that the electrostatic force between two charges in a vacuum is,

$F = \frac{1}{4\pi \varepsilon_{0}} \frac{{{q_1}{q_2}}}{{{r^2}}}$

Now in the above equation if we put,

$q_1=q_2=1C$ and $r=1m$, then

$F= \frac{1}{4\pi \varepsilon_{0}} = 9 \times 10^{9} N$

So, from the above formula, we can define 1 Coulomb as,

One Coulomb is that amount of charge that repels an equal and similar charge with a force of $ 9 \times 10^{9} N$ when placed in a vacuum at a distance of one meter from it.

In the cgs system unit of charge is esu of charge or statcoulomb.

One esu of charge is that charge which repels an identical charge in vacuum at a distance of 1 cm from it with a force of 1 dyne.

$1 \quad Coulomb = 3 \times 10^9 \quad statcoulomb$

Relative Permittivity (Dielectric Constant)

Before defining permittivity let consider a question. What will be the magnitude of the electrostatic force between two charges kept at the same distance

(a) in a vacuum

(b) in some medium (water, glass slab etc.)

The answer is the force between them is greatly affected. For example, consider two charges placed at the same distance in water and in the air. The force between the two charges in water becomes about $\frac{1}{80} th$ of the force between them in the air. This is because absolute permittivity of water is about 80 times as large as the absolute permittivity of free space.

Permittivity is a property of the medium which determines the electric force between two charges in the medium.

We know that according to Coulomb's law the force between two charges $q_1$ and $q_2$ placed in vacuum at a distance $r$ apart is given by

$F_{v} = \frac{1}{4\pi \varepsilon_{0}} \frac{{{q_1}{q_2}}}{{{r^2}}} \tag{1} $

When same charges are placed at same distance in a medium then the force between them becomes

$F_{m} = \frac{1}{4\pi \varepsilon} \frac{{{q_1}{q_2}}}{{{r^2}}} \tag{2}$

here $\varepsilon$ is called the absolute permittivity or just Ipermitivity of the medium. Dividing equation (1) by equation (2)

$$\frac{F_v}{F_m}=\frac{\frac{1}{4\pi \varepsilon_{0}} \frac{q_1 q_2}{r^2}}{\frac{1}{4\pi \varepsilon}\frac{q_1 q_2}{r^2}}=\frac{\varepsilon}{\varepsilon_{0}}$$

In the above equation the ratio $ \frac{\varepsilon}{\varepsilon_{0}} $is called the relative permittivity ($\varepsilon_{r}$) or dielectric constant ($\kappa $) of the given medium.

We now have the formula for relative permittivity of the medium i.e.,

$$\varepsilon_{r}=\kappa = \frac{\varepsilon}{\varepsilon_{0}}= \frac{F_v}{F_m} $$

From above equation can conclude that, when two charges are placed in a material medium of dielectric constant $ \kappa$, the force between them $\frac{1}{\kappa}$ times the force in a vacuum. That is

$$ F_m = \frac{F_v}{\kappa}$$

Relative permittivity is the factor by which the electric force between the charges is decreased relative to vacuum.

If we put $\varepsilon = \varepsilon_{0} \varepsilon_{r}$ or $\varepsilon = \varepsilon_{0} \kappa$ in equation (1) we get,

$$F_m = \frac{1}{4\pi \varepsilon_{0} \varepsilon_{r} }\cdot \frac{q_1 q_2}{r^2} = F_m = \frac{1}{4\pi \varepsilon_{0} \kappa }\cdot \frac{q_1 q_2}{r^2} $$

Coulombs law in vector form

In this section we'll learn about Coulomb's Law in vector form. From mechanics we know that force is a vector quantity. So force has a magnitude as well as direction. Coulomb's law is the law of electrostatics force between electric charges. Like other types of forces electrostatic force expressed by Coulomb's Law has magnitude as well as direction.

The direction of force between two charges depends on whether charges under consideration are like charges or opposite charges. Let us now understand this statement with the help of the figure given below.

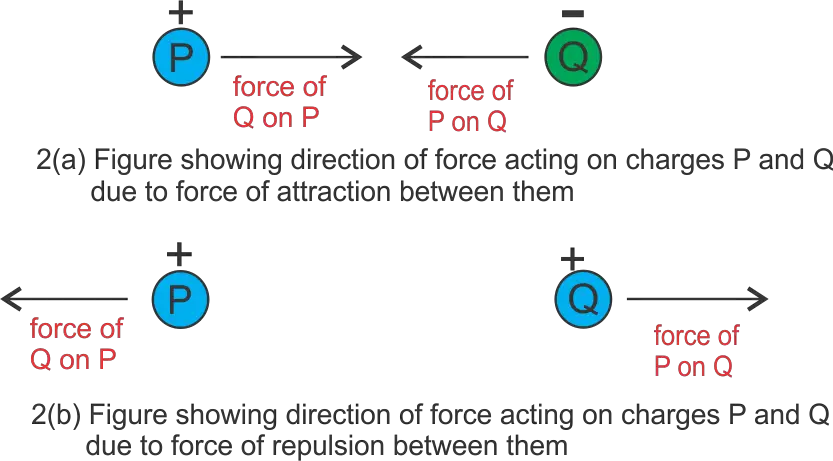
In figure (2a) we have two charged bodies $P$ and $Q$. These charged bodies carry opposite charge i.e., $P$ has a positive charge and $Q$ has a negative charge. We know that opposite charges attract each other. So there is a force of attraction between bodies $P$ and $Q$. Now $P$ exerts a force on $Q$ and this force acts towards body $P$ that is towards the left. Now $Q$ exerts a force on $P$ and this force acts towards body $Q$ that is towards the right.

Again in figure (2b), we have two charged bodies $P$ and $Q$. These charged bodies carry the same charge i.e., both $P$ and $Q$ have a positive charge. We know that the same charges repel each other. So there is a force of repulsion between bodies $P$ and $Q$. Now $P$ exerts a force on $Q$ and this force acts away from body $P$ that is towards the right. Now $Q$ exerts a force on $P$ and this force acts away from body $Q$ that is towards the left.

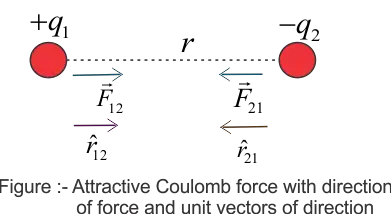
Let us now express Coulomb's Law in Vector form. For this let us consider a figure given below

Here we have two positive charges $q_1$ and $q_2$ kept at a distance $r$ from each other. Since both $q_1$ and $q_2$ have a positive charge they both would repel each other. Again from Newton's Third Law, we know that for every action there is an equal and opposite reaction. So here when charge $q_1$ exerts a force (action) on charge $q_2$, the charge $q_2$ also exerts an equal and opposite force (reaction) on charge $q_1$. In vector form, Coulomb's law may be expressed as

$\vec{F}_{21}=$ Force on charge $q_2$ due to $q_1$

Now you can read subscript of force $\vec{F}_{21}$ to determine the direction of the force. Here direction of force is from $q_1$ to $q_2$.

So in vector form we have

$\vec{F}_{21}= \frac{1}{4\pi \varepsilon_{0}} \frac{{{q_1}{q_2}}}{{{r^2}}} \hat{r}_{12}$

where, $ \hat{r}_{12} =\frac{\vec{r}_{12}}{r}$ is the unit vector in direction from $q_1$ to $q_2$.

So for force on charge $q_1$ due to $q_2$ ,

$\vec{F}_{12}=$ Force on charge $q_1$ due to $q_2$

So in vector form we have

$\vec{F}_{12}= \frac{1}{4\pi \varepsilon_{0}} \frac{{{q_1}{q_2}}}{{{r^2}}} \hat{r}_{21}$

where, $ \hat{r}_{21} =\frac{\vec{r}_{21}}{r}$ is the unit vector in direction from $q_2$ to $q_1$.

The same way we can write the Coulomb's Law in vector form for Columbian forces between unlike charges which are attractive in nature. Figure below gives the direction of force acting on $q_1$ and $q_2$.

Key points of Coulomb's law in vector form

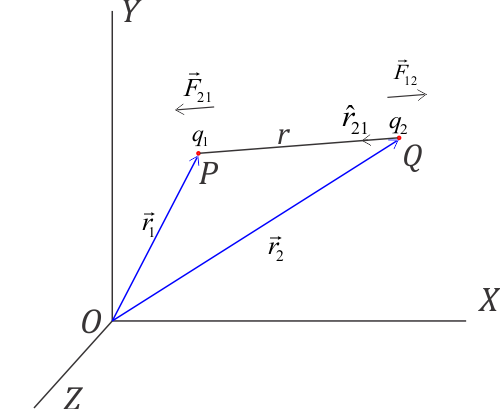
From vector form of Coulomb's Law, we can deduct following important information

1. From the above discussion we came to know that $\hat{r}_{21}= -\hat{r}_{12} $ which results in forces $\vec{F}_{21}= -\vec{F}_{12} $. This means that two charges exert equal and opposite force on each other. As discussed earlier electrostatic forces obeys newton's third law of motion.
2. Columbian forces act along a line joining the center of two charges. So they are an example of central forces.

Force between two charges in terms of their position vectors

\

To express force between two point charges in terms of their position vectors, consider two point charges $q_1$ and $q_2$ at points $P$ and $Q$ respectively. From the figure given above we can see that position vectors of points $P$ and $Q$ are $\vec OP = \vec{r_1}$ and $\vec OQ = \vec{r_2}$. Let us now join these two point charges $q_1$ and $q_2$ through a straight line. Let $r$ be the distance between these two point charges. Let $\hat {r}_{21}$ is the unit vector from charge $q_2$ to $q_1$, then force on charge $q_1$ doe to $q_2$ is given by \begin{equation*} \vec{F}_{12} = \frac{1}{4\pi \varepsilon_0}\cdot \frac{q_1q_2}{r^2}\hat {r}_{21} \end{equation*} We can rewrite above equation as \begin{equation} \label{eq:2} \vec{F}_{12} = \frac{1}{4\pi \varepsilon_0}\cdot \frac{q_1q_2}{r^3}(r\hat {r}_{21}) \end{equation} From the triangle law of vector addition we have $\vec{OQ}+\vec{QP}=\vec{OP}$ or $\vec{QP}=\vec{OP}- \vec{OQ}$.
Since $(\vec{QP}= r\hat {r}_{21})$,
So we have, $r\hat {r}_{21}= \vec{r}_1 - \vec{r}_2$ and $r=\left | \vec{r}_1 - \vec{r}_2 \right |$
In equation \begin{equation} \vec{F}_{12} = \frac{1}{4\pi \varepsilon_0}\cdot \frac{q_1q_2}{r^3}(r\hat {r}_{21}) \end{equation} putting
$r\hat {r}_{21}= \vec{r}_1 - \vec{r}_2$
and
$r=\left | \vec{r}_1 - \vec{r}_2 \right |$ ,
we get \begin{equation} \label{eq:3} \vec{F}_{12}=\frac{1}{4\pi \varepsilon_0}\cdot\frac{q_1q_2}{\left ( \left | \vec{r}_1 - \vec{r}_2 \right | \right )^3}\left ( \vec{r}_1 - \vec{r}_2 \right ) \end{equation} Similarly we can find the force on charge $q_2$ due to charge $q_1$ as \begin{equation*} \vec{F}_{21}=\frac{1}{4\pi \varepsilon_0}\cdot\frac{q_1q_2}{\left ( \left | \vec{r}_2 - \vec{r}_1 \right | \right )^3}\left ( \vec{r}_2 - \vec{r}_1 \right ) \end{equation*}

Coulombs law formula

From the above discussion, we have a fair knowledge of Coulomb's Law. It is a law explaining the electrostatic interaction between charged particles, objects or bodies. In this section, you get the gist of what we have studied so far. So, we have Coulomb's law formula which is given by the expression

$$F_v = \frac{1}{4\pi \varepsilon_{0}} \frac{{{q_1}{q_2}}}{{{r^2}}}= 9 \times 10^{9} \times \frac{{{q_1}{q_2}}}{{{r^2}}} $$ is in Newton

Above equation gives only the magnitude of the electrostatic force between two charged particles in vacuum.

If material medium exists between charged particles then we have

$F_{m} = \frac{1}{4\pi \varepsilon} \frac{{{q_1}{q_2}}}{{{r^2}}} $

Units used:- $q_1$ and $q_2$ are in Coulomb, $F$ is in Newton and $r$ is in metre.

Constant used:- $k=\frac{1}{4 \pi \varepsilon_0}=9\times 10^9 Nm^2C^{-2}$

Principle Of Superposition of electric charges

We know that Coulomb's law gives the electric force acting between two electric charges. What method or principle should we apply if we want to calculate the forces between many charges?

Principle of superposition gives the method to find force on a charge when system consists of large number of charges.

According to this principle when multiple charges are interacting the total force on a given charge is vector sum of forces exerted on it by all other charges.

This principle makes use of the fact that the forces with which two charges attract or repel one another are not affected by the presence of other charges.

If a system of charges has $n$ number of charges say $q_1$, $q_2$, ...................., $q_n$, then total force on charge $q_1 $ according to principle of superposition is
${\vec F_1} = {\vec F_{12}} + {\vec F_{13}} + ....... + {\vec F_{1n}}$
Where $ \vec F_{12} $ is force on $q_1$ due to $q_2$ and $ {\vec F_{13}} $ is force on $q_1$ due to $q_3$ and so on.

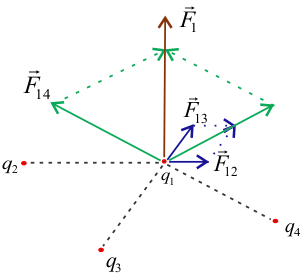
Please note that charges under consideration in above figure are all negative charges. Electrostatic Forces between these charges are force of repulsion as like charges repel each other.

Similarly we can calculate $ {\vec F_{12}} $ , $ {\vec F_{13}} $ , .................. $ {\vec F_{1n}} $ from Coulomb's law i. e.
$$ \vec F_{12} =\frac{q_{1}q_{2}{\widehat{r}_{12}}}{4\pi \varepsilon _{0}r_{12}^{2}}$$
to,
$$ {\vec F_{1n}} =\frac{q_{1}q_{2}{\widehat{r}_{1n}}}{4\pi \varepsilon _{0}r_{1n}^{2}}$$

The total force $F_1$ on the charge $q_1$ due to all other charges is the vector sum of the forces ${\vec F_{12}}$ , $ {\vec F_{13}}$ , ................................. $ {\vec F_{1n}} $.
$${\vec F_1} = {\vec F_{12}} + {\vec F_{13}} + ....... + {\vec F_{1n}}$$
$${{\vec F}_1} = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{{{q_1}{q_2}}}{{r_{12}^2}}{{\hat r}_{21}} + \frac{{{q_1}{q_3}}}{{r_{13}^2}}{{\hat r}_{31}} + ......\frac{{{q_1}{q_n}}}{{r_{1n}^2}}{{\hat r}_{n1}}} \right]$$

or,

$${{\vec F}_1} = \frac{{{q_1}}}{{4\pi {\varepsilon _0}}}\sum\limits_{i = 1}^n {\frac{{{q_i}}}{{r_{1i}^2}}{{\hat r}_{i1}}} $$

Here the vector sum done using parallelogram law of vector addition of vector. Same way force on any other charge due to other charges say on $q_2$, $q_3$ etc. can found using this method.

Concept Map

---

• Notes
  • Electric Charge , Basic properties of electric charge and Frictional Electricity
  • Electrical and electrostatic force
  • Coulomb's Law (with vector form)
  • Principle Of Superposition
  • Electric Field & Calculation of Electric Field
  • Electric Field Due to Line Charge
  • Electric Field Lines
  • Electric Flux
  • Electric Dipole and Dipole Moment
  • Electric Dipole Field
• Assignment
  • Electrostatics Multiple Choice Questions
  • Electrostatics Problems
  • Electrostatics Questions and answers
  • Electrostatics Important Questions for Class 12

---

---

Latest Updates Synthetic Fibres and Plastics Class 8 Practice questions

---

Class 8 science chapter 5 extra questions and Answers

---

Mass Calculator

---

3 Fraction calculator

---

Garbage in Garbage out Extra Questions7

---