Latest Articles

Electric dipole field

9. Electric Dipole

Electric dipole is a pair of equal and opposite charges, +q and -q, separated by some distance 2a.
Total charge of the dipole is zero but electric field of the dipole is not zero as charges q and -q are separated by some distance and electric field due to them when added is not zero.

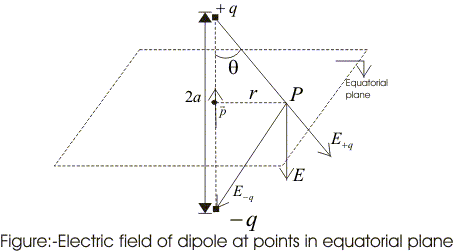
(A)Field of an electric dipole at points in equitorial plane
We now find the magnitude and direction of electric field due to dipole.
P point in the equitorial plane of the dipole at a distance r from the centre of the dipole. Then electric field due to +q and -q are $$\boldsymbol{E_{-q}}=\frac{-q\boldsymbol{\widehat{P}}}{4\pi \epsilon _{0}(r^{2}+a^{2})}$$
(1a) $$\boldsymbol{E_{+q}}=\frac{q\boldsymbol{\widehat{P}}}{4\pi \epsilon _{0}(r^{2}+a^{2})}$$
(1b)
and they are equal
Pˆ = unit vector along the dipole axis (from -q to +q)
From fig we can see the direction of E_+q and E_-q. Their components normal to dipole cancel away and components along the dipole add up.
Dipole moment vector points from negative charge to positive charge so in vector form.
E = -(E_+q + E_-q) cos θ


                                        (2)
At large distances (r>>a), above equation becomes
$$\boldsymbol{E}=\frac{-2qa\boldsymbol{\widehat{P}}}{4\pi \epsilon _{0}r^{3}} $$
                                        (3)
and they are equal

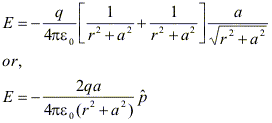
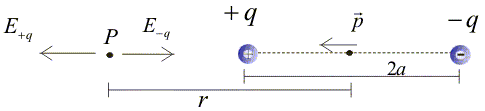
(B) Field of an electric dipole for points on the axis
Let P be the point at a distance r from the centre of the dipole on side of charge q. as shown in the fig.
$$\boldsymbol{E_{-q}}=\frac{-q\boldsymbol{\widehat{P}}}{4\pi \epsilon _{0}(r+a)^{2}}$$
(4a)
Pˆ = unit vector along the dipole axis (from -q to +q)
also
$$\boldsymbol{E_{+q}}=\frac{q\boldsymbol{\widehat{P}}}{4\pi \epsilon _{0}(r-a)^{2}}$$
(4b)
Total field at P is
E = E_+q + E_-q

(5)
for r>>a
$$\boldsymbol{E}=\frac{4qa\boldsymbol{\widehat{P}}}{4\pi \epsilon _{0}r^{3}} $$
(6)
For equation (3) and (6) charge q and dipole separation 2a appear in combination qa. This leads us to define dipole moment vector P of electric dipole. Thus, electric dipole moment P = q × 2a Pˆ (7)
Unit of dipole moment is Coulomb's meter (Cm).
In terms of electric dipole moment, field of a dipole at large distances becomes

(i) At point on equitorial plane (r>>a)
E = -P/4πε₀r³
$$\boldsymbol{E}=\frac{-\boldsymbol{P}}{4\pi \epsilon _{0}(r)^{3}} $$
(ii) At point on dipole axis (r>>a)
$$\boldsymbol{E}=\frac{2\boldsymbol{P}}{4\pi \epsilon _{0}(r)^{3}} $$

Note:-
(i) Dipole field at large distances falls off as 1/r³
(ii) Both the direction and magnitude of dipole an angle between dipole moment vector P and position vector r

(C) Dipole in a uniform external field
Consider a dipole in a uniform electric field E whose direction makes an angle θ with dipole axis (line joining two charges)
Force F₁ of magnitude qE, acts on positive charge in direction of electric field and a force F₂ of same magnitude acts on negative charge but it acts in direction opposite to F₁.
Resultant force on dipole is zero, but since two forces do not have same line of action they constitute a couple.
We now calculate torque (r × F) of these forces about zero.

Torque of F₁ about O is
τ₁= OB × F₁
     = q (OB × E)

Torque of F₂ about O is
τ₂ = OA × F₂
     = -q(OA × E)
     = q(AO × E)

net torque acting on dipole is
τ = τ₁ + τ₂
     = q(OB+ AO) × E
     = q (AB × E)

AB = 2a and p = 2qa (dipole moment)
τ =p × E
Direction of torque is perpendicular to the plane containing dipole axis and electric field.
Effect of torque is to rotate the dipole to a position in which dipole moment p is parallel to E the electric field vector is shown above in figure b and for uniform electric field dipole is in equilibrium in this position.
magnitude of this torque is
τ = |τ| = pE sinθ

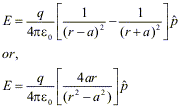
Examples

Question 1
Two point charges q₁ and q₂are located with points having position vectors r₁ and r₂
(1) Find the position vector r₃ where the third charge q₃ should be placed so that force acting on each of the three charges would be equal to zero.
(2) Find the amount of charge q₃

Question 2
Consider a thin wire ring of radius R and carrying uniform charge density λ per unit length.
(1) Find the magnitude of electric field strength on the axis of the ring as a function of distance x from its centre.
(2) What would be the form of electric field function for x>>R.
(3) Find the magnitude of maximum strength of electric field.

Question 3
Two equally charged metal balls each of mass m Kg are suspended from the same point by two insulated threads of length l m long. At equilibrium, as a result of mutual separation between balls, balls are separated by x m. Determine the charge on each ball.