

In this article we would find the electric field due to a line charge . By line charge we mean that charge is distributed along the one dimensional curve or line $l$ in space. Here in this article we would find electric field due to finite line charge derivation for two cases
We would be doing all the derivations without Gauss’s Law. At the same time we must be aware of the concept of charge density. Here since the charge is distributed over the line we will deal with linear charge density given by formula
$$\lambda=\frac{q}{l}N/m$$
Positive charge $Q$ is distributed uniformly along y-axis between $y=-a$ and $y=+a$. We have to find electric field due to line charge at point $P$ on the x-axis at a distance $x$ from the origin.
Figure below shows the situation and we have to find the electric field at point $P$ due to continuous distribution of charge.
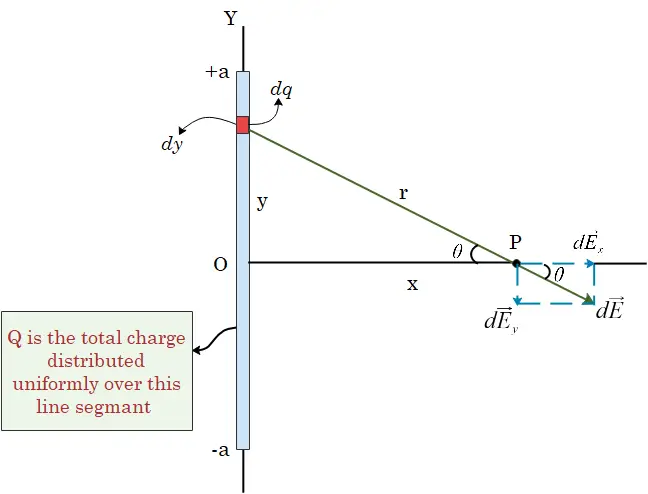
We can solve the problem by mentally dividing the line segment of length $2a$ into differential parts of length $dy$, with each of these lengths carrying a differential amount of charge $dq$. If $\lambda$ is the linear charge density then,
$dq=\lambda dy$
Where
$\lambda=\frac{Q}{2a}$
Here it is important to note that x-axis is the perpendicular bisector of our line segment. So, our point $P$ is at a distance $x$ from the mid point $O$ of the charged line segment.
The distance $r$ from the segment at height $y$ to the field point $P$ is
$r=\sqrt{x^2+y^2}$
Which is obtained using Pythagoras Theorem where $r$ is the hypotenuse, $y$ is the opposite side and $x$ is the adjacent side of the right angle triangle.
So, magnitude of the field at point $P$ due to segment of height $y$ is
$$dE=\frac{1}{4\pi \epsilon_0}\frac{dQ}{r^2}=\frac{1}{4\pi \epsilon_0}\frac{Q}{2a}\frac{dy}{(x^2+y^2)}$$
From the figure given above we can clearly see the x and y components of this field. Here component $d\vec{E}_x$ is perpendicular to the charged line segment and $d\vec{E}_y$ is parallel to it.
On resolving $d\vec{E}$ into x and y components we get
$d\vec{E}_x=dE\cos\theta$
$d\vec{E}_y=-dE\sin\theta$
Where,
$\cos\theta=\frac{adjacent}{hypotanuse}=\frac{x}{r}$
$\sin\theta=\frac{opposite}{hypotanuse}=\frac{y}{r}$
Hence,
$$d\vec{E}_x=\frac{1}{4\pi\epsilon_0}\frac{Q}{2a}\frac{xdy}{(x^2+y^2)^{3/2}}$$
$$d\vec{E}_y=\frac{1}{4\pi\epsilon_0}\frac{Q}{2a}\frac{ydy}{(x^2+y^2)^{3/2}}$$
From the symmetry of the configuration, the component of $d\vec{E}$ parallel to the line charge distribution is zero. When a positive test charge is placed at P, the upper half of the charge line apply force on it along downward direction, while the lower half applies a force of equal magnitude in upward direction. This, the top and lower parts of the segment contribute equally to the total field at P, according to symmetry.
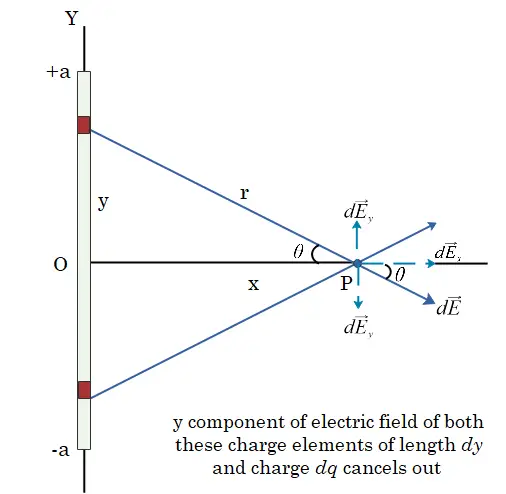
So, from this symmetry argument
$d\vec{E}_y=0$
The net electric field at point $P$ due to this line segment is perpendicular to the line segment and can be found if we calculate the sum of the fields from all segments along the line. For this, we must integrate from $y = -a$ to $y = +a$. SO,
$$E_x = \int_{-a}^{+a} dE_x$$
Or,
$$E_x =\frac{1}{4\pi\epsilon_0}\frac{Q}{2a}\int_{-a}^{+a} {\frac{xdy}{(x^2+y^2)^{3/2}}}$$
$$E_x =\frac{1}{4\pi\epsilon_0}\frac{Q}{2a}\int_{-a}^{+a} {\frac{xdy}{(x^2+y^2)^{3/2}}}$$
$y=x\tan\theta$
$dy=xsec^2\theta d\theta$
$$=\frac{x^2}{4\pi\epsilon_0}\frac{Q}{2a}\int{\frac{sec^2\theta d\theta}{(x^2+x^2tan^2\theta)^{3/2}}}$$
We will now solve for this integral
$$I=\int{\frac{sec^2\theta d\theta}{(x^2+x^2tan^2\theta)^{3/2}}}$$
$$I=\int{\frac{sec^2\theta d\theta}{(x^2+x^2tan^2\theta)^{3/2}}}=\int{\frac{sec^2\theta d\theta}{[x^2(1+tan^2\theta)]^{3/2}}}$$
$$I=\int{\frac{sec^2\theta d\theta}{x^3(sec^2\theta)^{3/2}}}$$
$\because 1+tan^2\theta=\sec^2\theta$
$$I=\frac{1}{x^3}\int{\frac{sec^2\theta}{\sec^3\theta}}$$
$$I=\frac{1}{x^3}\int{\cos\theta d\theta}$$
$$I=\frac{1}{x^3}\sin\theta$$
$$\because y=x\tan\theta \Rightarrow \frac{y}{x}=\tan\theta \Rightarrow \arctan\frac{y}{x}=\theta$$
$$I=\frac{1}{x^3}sin \left(\arctan\frac{y}{x}\right )$$
$\left (\arctan\frac{y}{x} \right )$ ia an angle whose tangent function $=\frac{y}{x}$
Considering the sides of the right triangle. We have opposite side equal to y, adjacent side equal to x and hypotenuse $\sqrt{x^2+y^2}$
Therefore sine of this angle $= \frac{opposite\; side}{hypotenuse}=\frac{y}{\sqrt{x^2+y^2}}$
Our integral becomes
$$I=\frac{1}{x^3}\frac{y}{\sqrt{x^2+y^2}}$$
So, putting the integral result in equation for $E_x$ and applyingthe limits we get
$$E_x=\frac{x^2}{4\pi\epsilon_0}\frac{Q}{2a}\left [\frac{1}{x^3}\frac{y}{\sqrt{x^2+y^2}}\right ]_{-a}^{a}$$
$$E_x=\frac{1}{4\pi\epsilon_0}\frac{Q}{2a}\left [\frac{1}{x}\frac{y}{\sqrt{x^2+y^2}}\right ]_{-a}^{a}$$
$$E_x=\frac{1}{4\pi\epsilon_0}\frac{Q}{2a}\frac{1}{x}\left [\left (\frac{a}{\sqrt{x^2+a^2}}-\frac{(-a)}{\sqrt{x^2+a^2}}\right )\right ]$$
$$E_x=\frac{1}{4\pi\epsilon_0}\frac{Q}{2a}\frac{1}{x}\left [ \frac{2a}{\sqrt{x^2+a^2}}\right]$$
$$E_x=\frac{1}{4\pi\epsilon_0}\frac{Q}{x\sqrt{x^2+a^2}}$$
In vector form above electric field is written as $$\vec E=\frac{1}{4\pi\epsilon_0}\frac{Q}{x\sqrt{x^2+a^2}}\hat{i}$$ $\vec E$ points away from the line charge if charge on rod is positive and towards the line charge if charge on it is negative.
From the above equation,

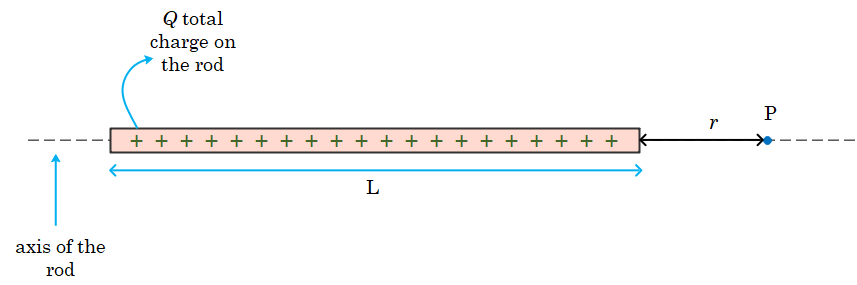
In this case our problem is to find the electric field due to uniformly charged rod of length $L$ at a point $P$ at distance $r$ from one end of the rod assuming that $Q$ is the total positive charge on the rod as shown below in the figure.
Let's start by defining a coordinate system for our problem. We'll use an x-coordinate system because we're dealing with a one-dimensional case. Let's suppose the left side of the rod is at the origin. Our infinitesimal charge element will be $x$ distance away from the origin in this coordinate system, and the length of this infinitesimal charge element will be $dx$ as shown in the figure.
Charge $dq$ on the infinitesimal length element $dx$ is
$dq=\frac{Q}{L}dx$
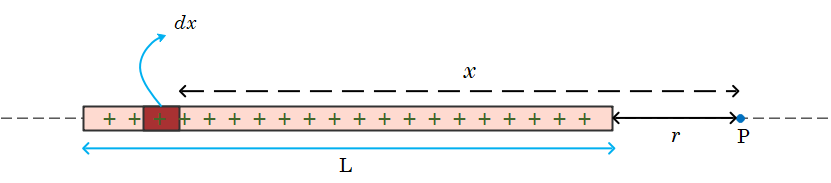
This $dq$ can be regarded as a point charge, hence electric field $dE$ due to this element at point $P$ is given by equation,
$$dE=\frac{dq}{4\pi\epsilon_0 x^2}$$
$$\Rightarrow \,\, dE=\frac{(Q/Lx^2)dx}{4\pi\epsilon_0}$$
and this field is generated at our point of interest $P$ is in radially outward direction as shown in the figure. Once we have found the electric field due to this charge element we would be able to find the electric field due to all other such infinitesimally small charged elements.
The net electric field strength at point $P$ can be given by integrating this expression over the whole length of the rod.
$$E=\int dE$$
It must be noted that electric field at point $P$ due to all the charge elements of the rod are in the same direction
$$E=\int dE =\int_r^{r+L}\frac{1}{4\pi\epsilon_0}\frac{Q}{Lx^2}dx$$
$$E=\frac{Q}{4\pi\epsilon_0L}\int_r^{r+L}\frac{1}{x^2} $$
$$E=\frac{Q}{4\pi\epsilon_0L}\left[ -\frac{1}{x} \right ]_r^{r+L}$$
$$E=\frac{Q}{4\pi\epsilon_0L}\left [ \frac{1}{r}-\frac{1}{r+L} \right ] $$
This is our required expression.
Visit this link for a good detailed video on Electric field of a charged rod along its Axis (uncc.edu)