In this article, we would learn about charge density and its formulas and would also solve some problems related to this concept. We encounter electric charge density while calculating electric field from various continuous charge distributions like linear, surface and volume. We also need the concept of charge density while studying current electricity.
What is Charge Density?
To understand charge density we must have an idea about the concept of density. Mass per unit volume of any object gives the density of that object. Similarly, we could think of charge density as charge per unit length, surface or volume depending on the type of continuous charge configuration.
In order to describing continuous charge density where we have a of number of discrete charges, is analogous to continuous mass density, which actually consists of a large number of separate/discrete molecules.
Charge Density Formulas
Lots of time while solving problems it is not enough to know about total charge on the charged object. Sometimes we need to know about how that charge is distributed. It measures the amount of electric charge
- Per unit length (linear charge density)
- Per unit area (surface charge density)
- Per unit volume (volume charge density)
Linear Charge Density
Linear charge density is defined for objects like thin wires, charged rods or thin cylinders. In this configuration, the charge is distributed linearly.
Linear charge density is defined a charge per unit length of the object and is measured in $C/m$. We use Greek letter $\lambda$ to represent linear charge density.
Formula
$$\lambda=\frac{q}{l}$$
Where, $q$ is the total charge and $l$ is the total length over which this charge is distributed uniformly.
If the charge density varies over the length of the object then linear charge density is defined using calculus. In this case, we would consider infinitesimal length element $dl$ containing infinitesimal amount of charge $dq$ and linear charge density, in this case, would be
$$\lambda = \frac{dq}{dl}$$
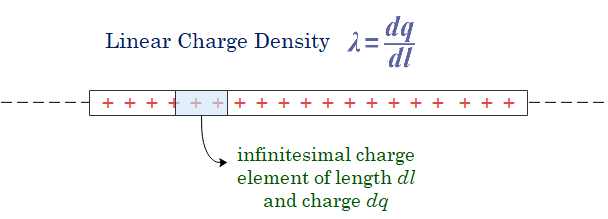
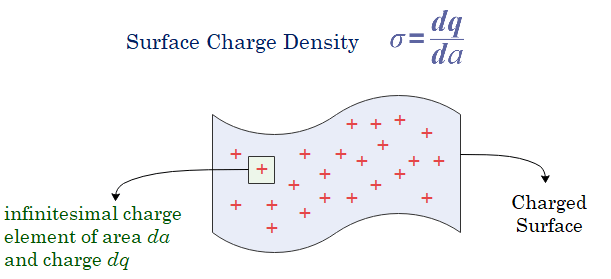
Surface Charge Density
A surface charge density, can be determined for objects like flat plates or the surfaces of cylinder and sphere, hemisphere etc. The quantity of charge per unit area of the object is defined as surface charge density. It’s unit is $N/m^2$ and is represented by Greek letter $\sigma$.
Formula
If the charge $q$ is distributed uniformly over a surface of area $a$ then,
$$\sigma=\frac{q}{a}$$
If the distribution of charge or charge density varies over the area of the surface under consideration we would consider infinitesimal area element $da$ containing infinitesimal amount of charge $dq$ and surface charge density in this case would be
$$\sigma = \frac{dq}{da}$$
Volume Charge Density
Finally, a volume charge density, can be defined for objects with charge spread throughout their volume. This is the charge per volume unit of the thing. This is true if the charge is uniformly distributed. The quantity of charge per unit volume of the object is defined as volume charge density. It’s unit is $N/m^3$ and is represented by Greek letter $\rho$.
Formula
If the charge $q$ is distributed uniformly over a surface of volume $V$ then,
$$\rho=\frac{q}{V}$$
If the distribution of charge or charge density varies over the volume of the charged object under consideration we would consider infinitesimal volume element $dV$ containing infinitesimal amount of charge $dq$ and volume charge density in this case would be
$$\rho = \frac{dq}{dV}$$
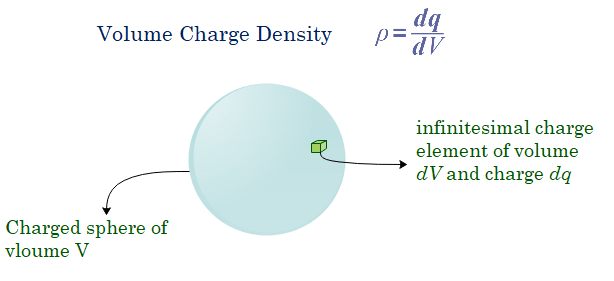
Solved Example Questions
Question 1 A long thin wire of length 30 cm has a total charge of $20\mu C$ distributed uniformly over the length of the wire. Find the linear charge density of the wire?
Solution:
It is given in the question that
$q=20\mu C=20 \times 10^{-6}$
$l=30 cm = .3m$
And we have to calculate the linear charge density $\lambda$
Linear charge density formula is
$\lambda=\frac{q}{l}$
Putting in the values we get
$\lambda=\frac{q}{l}=\frac{20 \times 10^{-6}}{.3}=6.67\times 10^{-5}C/m$
Question 2 Find the charge and charge density on the surface of conducting sphere of radius 15.2cm and potential 215V??
Solution
Part a
To calculate the charge we will use the relation
$$V=k\frac{q}{r}$$
Rearranging it for $q$ we get
$$q=\frac{rV}{k} \tag{1}$$
Learn more about electric Potential
It is given in the question that
$V=125V$,
$r=15.2 cm=.152 m$ and
We know that constant $k=9\times 10^9Nm^2/C^2$
Putting in these values in equation (1)
$$q=\frac{rV}{k} = \frac{0.152m \times 215V}{9\times 10^9Nm^2/C^2}=3.6 nC$$
Part b
Surface charge density is given by formula
$\sigma=\frac{q}{a}=\frac{q}{4\pi r^2}$
Or,
$\sigma=\frac{3.6\times 10^{-9}C}{4\times 3.14 \times(0.152m)^2}=12.4 nC/m^2$
For learning more you can visit Charge density Wikipedia
 Skip to content
Skip to content