What is heisenberg uncertainty principle?
Heisenberg Uncertainty Principle or indeterminacy principle was given by German scientist Warner Heisenberg according to which position and momentum of an object can not be measured simultaneously. So if we measure the position of some particle more precisely then its momentum is measured less precisely and vice verse.Heisenberg uncertainty principle can be written as follows
If a measurement of position of particle is made with precision $\Delta x$ and a simultaneous measurement of linear momentum is made with precision $\Delta {p_x}$ then the product of two uncertainties can never be greater than $\frac{h}{{4\pi }}$
\(\Delta x\Delta {p_x} \ge \frac{h}{{4\pi }}\) (1)
In other words we can say that it is physically impossible to measure simultaneously the exact position and exact linear momentum of a particle. So if $\Delta x$ is very small then $\Delta {p_x}$ is very large and vice versa. Here $\Delta x$ and $\Delta {p_x}$ are the indeterminateness in our knowledge of coordinate and the momentum of the particle.
Here when talking about uncertainty principle we are not talking about the technical difficulties of measuring. It is just that experiments can not yield greater accuracy than that allowed by the Heisenberg principle.
To understand this consider a thought experiment where you want to measure the position and linear momentum of an electron as accurately as you can. One w ay of doing this is using a powerful light microscope. To understand further consider the figure given below
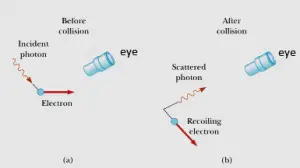
Now to see the electron and measure its position at least one photon of light must bounce it and pass through the microscope into your eye as shown below in figure a) and b) . Again when this photon strikes the electron , it transfers some unknown amount of its momentum to the electron. Thus in the process of accurately measuring the position of the electron (that is by making $\Delta x$ very small ) you somehow disturb the electron’s momentum to some indeterminable extent (that is you made $\Delta p_{x}$ very large)
If $\lambda$ is the wavelength of the incoming photon then its momentum would be $\frac{h}{\lambda}$ . Now as a result of collision , the momentum of the electron is disturbed. So the photon might transfer a part or all of its momentum along x-axis to the electron. Therefore the uncertainty in electron’s momentum after the collision could be as great as the momentum of incoming photon that is $\Delta p_{x}=\frac{h}{\lambda}$ . Now electron also possess wave properties so we should be able to determine the electron’s position within one wave length of light being used to view it, so $\Delta x = \lambda$. Multiplying these two uncertainties give
$\Delta x \Delta p_{x}=\lambda(\frac{h}{\lambda})=h$
The value h represents the minimum in the product of the uncertainties. Because the uncertainty can always be greater than this minimum, we have
\(\Delta x\Delta {p_x} \ge h\)
Apart from the numerical factor $\frac{1}{4\pi }$ introduced by Heisenberg’s more precise analysis this inequality agrees with equation 1.
Another form of the uncertainty relationship sets a limit on the accuracy with which the energy $E$ of a system can be measured in a finite time interval $\Delta t$:
$\Delta E \Delta t \ge \frac{h}{4 \pi}$ (2)
This equation tells us that energy of a particle can not be measured with complete precision in a very short interval of time. Thus when an electron is viewed as a particle , the uncertainty principle tells us that
- its position and velocity can not be known precisely at the same time
- its energy can be uncertain for a period that is given by $\Delta t = \frac{h}{4 \pi \Delta E}$
The heisenberg uncertainty principle summary
Heisenberg Uncertainty Principle or indeterminacy principle was given by German scientist Warner Heisenberg according to which position and momentum of an object can not be measured simultaneously. So if we measure the position of some particle more precisely then its momentum is measured less precisely and vice verse.
This article is about the summary of the uncertainty principle not about the conceptual explanation of it.
- If a measurement of position is made wit accuracy $\Delta x$ , and if the measurement of momentum is made simultaneously with accuracy $\Delta p$, then the product of two errors can never be smaller than a number of order $\hbar$
$\Delta E \Delta t \geqslant (\sim \hbar)$ (1) - Similarly if the energy of a system is measured to accuracy $\Delta E$ , then the time to which this measurement refers must have a minimum uncertainity given by
$\Delta p \Delta x \geqslant (\sim \hbar)$ (2) - More generally, if $\Delta q$ is the error in the measurement of any co-ordinate , and $\Delta p$ is the error in its canonically conjugate momentum , we have
$\Delta p \Delta q \geqslant (\sim \hbar)$ (3) - The relation between the range of positions $\Delta x$ and the range of wave numbers $\Delta k$ appearing in the wave packet is
$\Delta x \Delta k \geqslant 1 $ (4) - Uncertainty principle is obtained , when the following quantum mechanical interpretations of the quantities appearing in above equations are taken into account
- The de Brogli equation $p=\hbar \lambda$ creates a relationship between wave number and momentum which is not present in classical mechanics
- Whenever either momentum or the position of an electron is measured ,the result is always some definte number. A clasical wave packet always cover a range of wave numbers.
- $\Delta x$ is a measure of minimum uncertainty , or lack of complete determinism of , the position that can be ascribed to the electron.
- $\Delta k$ is a measure of minimum uncertainty , or lack of complete determinism of the momentum that can be ascribed to it.
Relation of spreading wave packet to uncertainty principle
- narrower the wave packet to begin with , the more rapidly it spreads
- because of confinement of the packet within the region $x_0$ the Fourier analysis contains many waves of length of the order of $\Delta x_0$ , hence momenta $p\simeq \frac{\hbar}{\Delta x_0}$
Therefore,
$\Delta v \simeq \frac{p}{m}\simeq \frac{\hbar}{m\Delta x_0}$ - Although average velocity of the packet is equal to the group velocity, there is still a strong chance that the actual velocity will fluctuate about this average by the above amount.
- The distance covered by the particle is not completely determined , but vary as much as
$\Delta x \simeq t\Delta v \simeq \frac{\hbar t}{m\Delta x_{0}}$ - The speed of the wave packet may therefore be regarded as one of the manifestations of the lack of complete determination of the initial velocity necessarily associated with a narrow wave packet.
Relation of stability of atoms to uncertainty principle
- From uncertainty principle if an electron is localized, it must have on the average , a high momentum, and hence a high kinetic energy.
- It takes energy to localize a particle.
- According to uncertainty principle, it takes a momentum $p\simeq \frac{\hbar}{\Delta x}$ , hence an enargy $E=\frac{p^{2}}{2m}\simeq \frac{\hbar^2}{2m(\DElta x)^2}$ to keep an electron localized within the region $\Delta x$ .
- This momentum creates a pressure , which tends to oppose localization of the electron.
- In an atom , the pressure is opposed by the force attracting the electron back to the nucleus.
- Thus the electron will come to equilibrium where the attractive forces balances the effective pressure and , this way the mean radius of the lowest quantum state is determined.
- Point of balance can be found from the condition that the total energy must be minimum.
- Thus we have
$W\simeq \frac{\hbar^2}{2m(\Delta x)^2}-\frac{e^2}{\Delta x}\\
\Delta x \simeq \frac{\hbar^2}{me^2}$
This result is just the radius of first Bohr orbit although not exact but qualitative. - The limitation on the localizability of the electron is inherent in the wave particle nature of matter.
- In order to have an electron in very small space, we must have very high Fourier components in its wave function and ,therefore, the possibility of very high momenta.
- There is no way to force an electron to occupy a well defined position and still remain at rest.
Question
Show that the uncertainty relation forces us to reject the semi classical Bohr model for the hydrogen atom
Solution
In Bohr atom model we deal with the electron as a classical particle. The allowed orbits are defined by the quantization rules:
The radius r of a circular orbit and the momentum $p = mv$ of the rotating electron must satisfy $pr = n\hbar (n = 1,2,3,….)$. To consider an electron’s model in classical terms , the uncertainties in its position and momentum must be negligible when compared to $r$ and $p$. In other words $\Delta x \ll r$ and $\Delta p \ll p$
This implies
$\frac{{\Delta x}}{r}\frac{{\Delta p}}{p} \ll 1$ (1)
On the other hand , the uncertainty relation imposes
$\frac{{\Delta x}}{r}\frac{{\Delta p}}{p} \ge \frac{\hbar }{{rp}} \Rightarrow \frac{{\Delta x\Delta p}}{{rp}} \ge \frac{1}{n}$ (2)
So, equation 1 is incompatible with 2 , unless $n \gg 1$


