Two particle system and reduced mass

This article is about Two particle system and reduced mass. This topic comes under the chapter Dynamics of System of Particles. It is for B.Sc. students and comes under subject mechanics. For full chapter notes links
please visit this link
Dynamics of System of Particles

Two body problems with central forces can always be reduced to the form of one body problems.
Consider a system made up of two particles. For an observer in any inertial frame of refrence relative motion of these two particles can be represented by the motion of a fictitious particle.
The mass of this fictetious particle is known as the reduced mass of two particle system.
Consider a system of two particles of mass m₁ and m₂ respectively. Let O be the origin of any inertial frame of reference and r₁ and r₂ be the position vectors of these particles at any time t w.r.t. origin O as shown bellow in the figure.
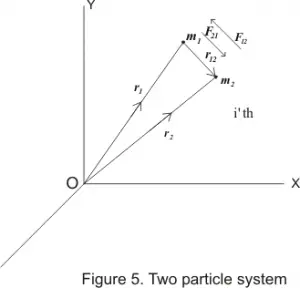
If no external force is acting on the system then the force acting on the system would be equal to mutual interaction between two particles. Let the force acting on m₁ due to m₂ be F₂₁ and force acting on m₂ due to m₁ be F₁₂ then equation of motion for particles m₁ and m₂ would be
\begin{equation}
{{\rm{F}}_{21}} = {m_1}\frac{{{d^2}{{\rm{r}}_1}}}{{d{t^2}}}
\end{equation}
and,
\begin{equation}
{{\rm{F}}_{12}} = {m_2}\frac{{{d^2}{{\rm{r}}_2}}}{{d{t^2}}}
\end{equation}
from 1 and 2
\begin{equation}
\frac{{{d^2}{{\rm{r}}_1}}}{{d{t^2}}} = \frac{{{{\rm{F}}_{21}}}}{{{m_1}}}
\end{equation}
and
\begin{equation}
\frac{{{d^2}{{\rm{r}}_2}}}{{d{t^2}}} = \frac{{{{\rm{F}}_{12}}}}{{{m_2}}}
\end{equation}
From the figure,
\begin{equation}
{{\rm{r}}_{12}} = {{\rm{r}}_{\rm{2}}} – {{\rm{r}}_1}
\end{equation}
so,
\begin{equation}
\frac{{{d^2}{{\rm{r}}_{12}}}}{{d{t^2}}} = \frac{{{d^2}{{\rm{r}}_2}}}{{d{t^2}}} – \frac{{{d^2}{{\rm{r}}_1}}}{{d{t^2}}}
\end{equation}
putting 3 and 4 in 6 we get
\begin{equation}
\frac{{{d^2}{{\rm{r}}_{12}}}}{{d{t^2}}} = \frac{{{{\rm{F}}_{12}}}}{{{m_2}}} – \frac{{{{\rm{F}}_{21}}}}{{{m_1}}}
\end{equation}
but from Newton’s first law of motion we have
F₂₁ = –F₁₂
then from equation 7 we have
$$\frac{{{d^2}{{\rm{r}}_{12}}}}{{d{t^2}}} = \frac{{{{\rm{F}}_{12}}}}{{{m_2}}} + \frac{{{{\rm{F}}_{12}}}}{{{m_1}}} = {{\rm{F}}_{12}}\left( {\frac{1}{{{m_1}}} + \frac{1}{{{m_2}}}} \right)$$
or,
$$\frac{{{d^2}{{\rm{r}}_{12}}}}{{d{t^2}}} = {{\rm{F}}_{12}}\left( {\frac{{{m_1} + {m_2}}}{{{m_1}{m_2}}}} \right)$$
$${{\rm{F}}_{12}} = \left( {\frac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}} \right)\frac{{{d^2}{{\rm{r}}_{12}}}}{{d{t^2}}}$$
or,
\begin{equation}
\rm{F}}_{12}} = \mu \frac{{{d^2}{{\rm{r}}_{12}}}}{{d{t^2}}}
\end{equation}
where,
$$\mu = \left( {\frac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}} \right)$$
is known as reduced mass of the system.
This equation 8 represents a one body problem , because it is similar to the equation of motion of single particle of mass μ at a vector distance r₁₂ from one of thr two particles, considered as the fixed centre of force.
Thus original problem involving two particle system has now been reduced to that of one particle system which is easier to solve then original two body problem.
Case 1. m₁ << m₂
If the mass of any one particle in two particle system is very very less in comparison to other particle like in earth-satellite system then reduced mass of the system would be
\begin{equation*}
\mu = \left( {\frac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}} \right) = \left( {\frac{{{m_1}}}{{1 + ({m_1}/{m_2})}}} \right)
\end{equation*}
or,
\begin{equation*}
\mu \approx \left( {1 – \frac{{{m_1}}}{{{m_2}}}} \right){m_1}
\end{equation*}
or, $\mu \approx {m_1}$
So the reduced mass of the two particle system would be equal to the particle having lesser mass.
Case 2. m₁ = m₂ = m
If the masses o8 the particles of a two particle system are same then
$$\mu = \left( {\frac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}} \right) = \frac{{{m^2}}}{{2m}} = \frac{m}{2}$$
Hence reduced mass of the system would be equal to the one half of the mass of a single particle.