This page provides a concise formula compilation on light reflection and refraction from Class 10 Science Chapter 9. A downloadable PDF formula sheet includes all essential formulas and key points. It facilitates efficient revision and subject mastery, serving as an invaluable study resource for board exams.
Revision Notes: Light – Reflection and Refraction
Reflection of Light
Laws of Reflection:
- The angle of incidence ($i$) is equal to the angle of reflection ($r$).
- The incident ray, the reflected ray, and the normal to the reflecting surface at the point of incidence all lie in the same plane.
Mirror Formula:
$$ \frac{1}{f} = \frac{1}{v} + \frac{1}{u} $$
Where:
- $f$ = focal length
- $v$ = image distance
- $u$ = object distance
Magnification (Mirrors):
$$ m = \frac{h’}{h} = -\frac{v}{u} $$
Where:
- $m$ = magnification
- $h’$ = image height
- $h$ = object height
Sign Conventions for Mirrors:
- Object distance ($u$): Always negative
- Image distance ($v$): Positive for virtual images, negative for real images
- Focal length ($f$): Positive for convex mirrors, negative for concave mirrors
- Image height ($h’$): Positive for erect images, negative for inverted images
Refraction of Light
Laws of Refraction (Snell’s Law):
$$ \frac{\sin i}{\sin r} = n $$
Where:
- $i$ = angle of incidence
- $r$ = angle of refraction
- $n$ = refractive index
Refractive Index:
$$ n = \frac{c}{v} $$
Where:
- $c$ = speed of light in vacuum
- $v$ = speed of light in the medium
Relative Refractive Index:
$$ n_{1,2} = \frac{V_2}{V_1} $$
Where $V_1$ and $V_2$ are the speeds of light in media 1 and 2 respectively.
Absolute Refractive Index:
$$ n_m = \frac{c}{V} $$
Lenses
Lens Formula:
$$ \frac{1}{f} = \frac{1}{v} – \frac{1}{u} $$
Where:
- $f$ = focal length
- $v$ = image distance
- $u$ = object distance
Magnification (Lenses):
$$ m = \frac{h’}{h} = \frac{v}{u} $$
Power of a Lens:
$$ P = \frac{1}{f} $$
Where $P$ is in diopters (D) and $f$ is in meters.
Net Power of Combined Lenses:
$$ P_{\text{net}} = P_1 + P_2 + P_3 $$
Where $P_1$, $P_2$, and $P_3$ are the powers of individual lenses.
Sign Conventions for Lenses:
- Object distance ($u$): Always negative
- Image distance ($v$): Positive for real images, negative for virtual images
- Focal length ($f$): Positive for convex lenses, negative for concave lenses
- Image height ($h’$): Positive for erect images, negative for inverted images
Additional Concepts
Magnification Sign Conventions:
- $m = -ve$ -> Inverted
- $m = +ve$ -> Erect
- $m < 1$ -> Diminished
- $m = 1$ -> Same size
- $m > 1$ -> Enlarged
Download this formula sheet as PDF
All formulas and concepts in tabular form
Mirror Formula and Magnification
| Category | Formula/Information | Description/Notes |
|---|---|---|
| Mirror Formula | $ \frac{1}{v} + \frac{1}{u} = \frac{1}{f} $ | Relates object distance ($u$), image distance ($v$), and focal length ($f$). |
| Magnification (m) | $ m = \frac{h’}{h} = -\frac{v}{u} $ | Magnification formula for mirrors, where $ h’ $ is the image height and $ h $ is the object height. |
Refraction and Refractive Index
| Category | Formula/Information | Description/Notes |
|---|---|---|
| Refraction | $ \frac{\sin i}{\sin r} = \text{constant} $ | Snell’s Law. |
| Refractive Index (R.I.) | $ \text{R.I.} = \frac{m_1}{m_2} $ | $ m_1 $ and $ m_2 $ are the speeds of light in two different media. |
| Absolute R.I. | $ \text{Absolute R.I.} = \frac{c}{V} $ | $ c $ is the speed of light in air (or vacuum), and $ V $ is the speed of light in the medium. |
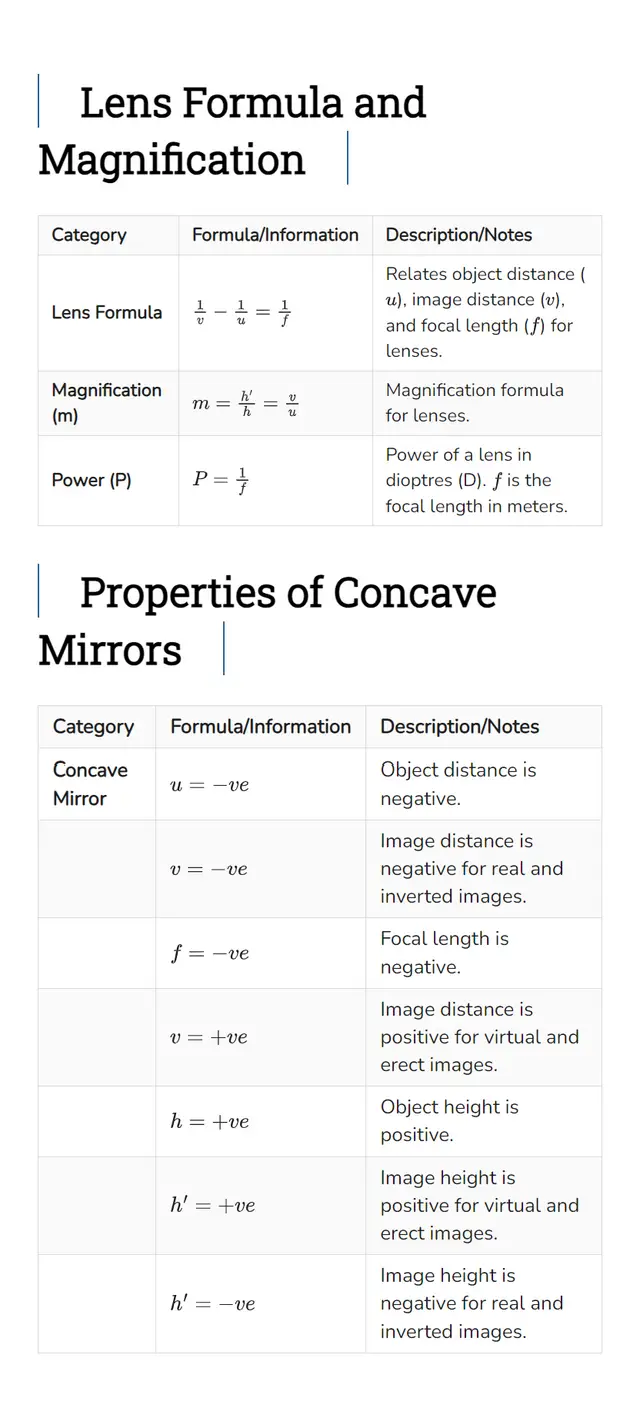
Lens Formula and Magnification
| Category | Formula/Information | Description/Notes |
|---|---|---|
| Lens Formula | $ \frac{1}{v} – \frac{1}{u} = \frac{1}{f} $ | Relates object distance ($u$), image distance ($v$), and focal length ($f$) for lenses. |
| Magnification (m) | $ m = \frac{h’}{h} = \frac{v}{u} $ | Magnification formula for lenses. |
| Power (P) | $ P = \frac{1}{f} $ | Power of a lens in diopters (D). $ f $ is the focal length in meters. |
Properties of Concave Mirrors
| Category | Formula/Information | Description/Notes |
|---|---|---|
| Concave Mirror | $ u = -ve $ | Object distance is negative. |
| $ v = -ve $ | Image distance is negative for real and inverted images. | |
| $ f = -ve $ | Focal length is negative. | |
| $ v = +ve $ | Image distance is positive for virtual and erect images. | |
| $ h = +ve $ | Object height is positive. | |
| $ h’ = +ve $ | Image height is positive for virtual and erect images. | |
| $ h’ = -ve $ | Image height is negative for real and inverted images. |
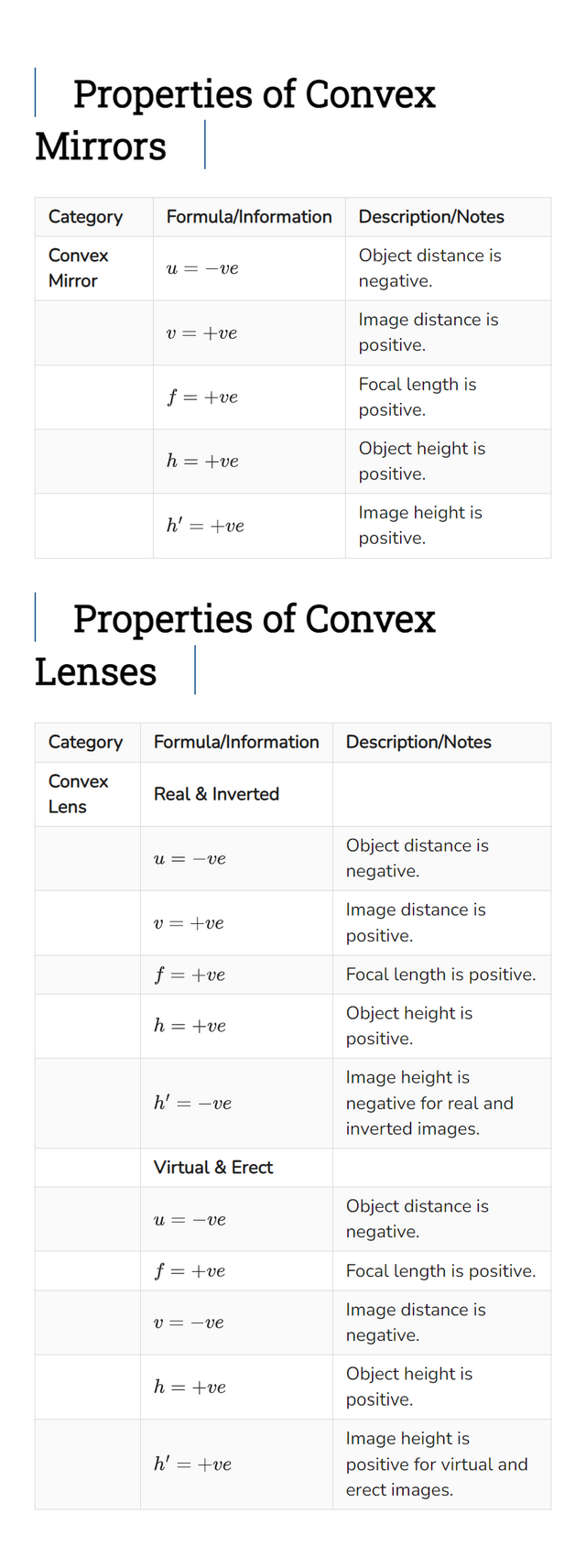
Properties of Convex Mirrors
| Category | Formula/Information | Description/Notes |
|---|---|---|
| Convex Mirror | $ u = -ve $ | Object distance is negative. |
| $ v = +ve $ | Image distance is positive. | |
| $ f = +ve $ | Focal length is positive. | |
| $ h = +ve $ | Object height is positive. | |
| $ h’ = +ve $ | Image height is positive. |
Properties of Convex Lenses
| Category | Formula/Information | Description/Notes |
|---|---|---|
| Convex Lens | Real & Inverted | |
| $ u = -ve $ | Object distance is negative. | |
| $ v = +ve $ | Image distance is positive. | |
| $ f = +ve $ | Focal length is positive. | |
| $ h = +ve $ | Object height is positive. | |
| $ h’ = -ve $ | Image height is negative for real and inverted images. | |
| Virtual & Erect | ||
| $ u = -ve $ | Object distance is negative. | |
| $ f = +ve $ | Focal length is positive. | |
| $ v = -ve $ | Image distance is negative. | |
| $ h = +ve $ | Object height is positive. | |
| $ h’ = +ve $ | Image height is positive for virtual and erect images. |
Properties of Concave Lenses
| Category | Formula/Information | Description/Notes |
|---|---|---|
| Concave Lens | $ u = -ve $ | Object distance is negative. |
| $ f = -ve $ | Focal length is negative. | |
| $ v = -ve $ | Image distance is negative. | |
| $ h = +ve $ | Object height is positive. | |
| $ h’ = +ve $ | Image height is positive for virtual and erect images. |
Magnification and Image Characteristics
| Category | Formula/Information | Description/Notes |
|---|---|---|
| Lenses | $ m = +ve \rightarrow \text{Virtual & Erect} $ | Magnification positive: virtual and erect image. |
| $ m = -ve \rightarrow \text{Real & Inverted} $ | Magnification negative: real and inverted image. | |
| $ m > 1 \rightarrow \text{Enlarged} $ | Magnification greater than 1: enlarged image. | |
| $ m < 1 \rightarrow \text{Diminished} $ | Magnification less than 1: diminished image. | |
| Mirrors | $ m = +ve \rightarrow \text{Virtual & Erect} $ | Magnification positive: virtual and erect image. |
| $ m = -ve \rightarrow \text{Real & Inverted} $ | Magnification negative: real and inverted image. | |
| $ m > 1 \rightarrow \text{Enlarged} $ | Magnification greater than 1: enlarged image. | |
| $ m < 1 \rightarrow \text{Diminished} $ | Magnification less than 1: diminished image. | |
| $ m = 1 \rightarrow \text{Same Size} $ | Magnification equal to 1: image is the same size as the object. |
Save and share these tables as image
Feel free to save these images or share them on social media among your friends.

Tips for Exam Preparation:
- Practice ray diagrams for both mirrors and lenses to understand image formation.
- Memorize the sign conventions and apply them consistently.
- Work through numerical problems using the mirror and lens formulas.
- Understand the conceptual difference between real and virtual images.
- Review the derivations of key formulas and practice applying them in different contexts.
These notes cover the essential formulas, sign conventions, and principles of reflection and refraction of light, which are critical for Class 10 exams. Adding diagrams at the appropriate places will help in visualizing the concepts better.
 Skip to content
Skip to content