Trigonometry ratios of complementary angles

Trigonometry is a branch of mathematics that deals with the relationship between the sides and angles of a triangle. In this article, we will discuss the trigonometry ratios of complementary angles.

Complementary angles

Complementary angles are two angles whose sum is 90 degrees

if A and B are complementary angles, then

$\angle A + \angle B = 90^0$
or
$\angle B = 90 – \angle A$

Hence A and 90 – A represent complementary angles

Complementary angles in Right angle triangle

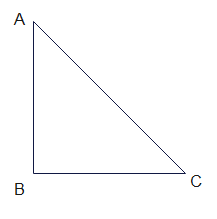
In a right angle triangle ABC
A+B+C=180
Now B=90
So A+C=90
Or 
A=90?C

Hence the acute angles in right angle triangle are complementary

Definition of Trigonometry Ratios of Complementary Angles

We know that trigonometric ratios of the acute angles A and C are given by

Angle C

$\sin C= \frac {\text{Perpendicular}}{\text{Hypotenuse}}=\frac {AB}{AC}$

$\csc C= \frac {\text{Hypotenuse}}{\text{Perpendicular}} =\frac {AC}{AB}$

$\cos C= \frac {\text{Base}}{\text{Hypotenuse}}=\frac {BC}{AC}$

$\sec C= \frac {\text{Hypotenuse}}{\text{Base}}=\frac {AC}{BC}$

$\tan C= \frac {\text{Perpendicular}}{\text{Base}}=\frac {AB}{BC}$

$\cot C= \frac {\text{Base}}{Perpendicular}=\frac {BC}{AB}$

Angle A

$\sin A= \frac {\text{Perpendicular}}{\text{Hypotenuse}}=\frac {BC}{AC}$

$\csc A= \frac {\text{Hypotenuse}}{\text{Perpendicular}} =\frac {AC}{BC}$

$\cos A= \frac {\text{Base}}{\text{Hypotenuse}}=\frac {AB}{AC}$

$\sec A = \frac {\text{Hypotenuse}}{\text{Base}}=\frac {AC}{AB}$

$\tan A= \frac {\text{Perpendicular}}{\text{Base}}=\frac {BC}{AB}$

$\cot A = \frac {\text{Base}}{Perpendicular}=\frac {AB}{BC}$

Now in a right angle triangle

C =90 -A

Therefore from Angle C ration’s will become

$\sin (90 -A)=\frac {AB}{AC}$

$\csc (90 -A) =\frac {AC}{AB}$

$\cos (90 -A) =\frac {BC}{AC}$

$\sec (90 -A) =\frac {AC}{BC}$

$\tan (90 -A) =\frac {AB}{BC}$

$\cot(90 -A) =\frac {BC}{AB}$

From these two equations we can find that

sin(A) = cos(90° – A)
cos(A) = sin(90° – A)
tan(A) = cot(90° – A)
cot(A) = tan(90° – A)
sec(A) = csc(90° – A)
csc(A) = sec(90° – A)

The above is the called the trigonometric ratio’s of the complementary angles

Examples of Trigonometry Ratios of Complementary Angles

Let us take an example of a right triangle with an acute angle A measuring 30 degrees. The complementary angle B will measure 60 degrees.

Using the formulas, we can find the trigonometry ratios of angle A and angle B.

sin(30°) = cos(60°) = 1/2
cos(30°) = sin(60°) = $\frac {\sqrt 3}{2}$
tan(30°) = cot(60°) = $\frac {1}{\sqrt 3}$
cot(30°) = tan(60°) = $\sqrt 3$
sec(30°) = csc(60°) = $\frac {2}{\sqrt 3}$
csc(30°) = sec(60°) = 2

Similarly, for an acute angle A measuring 45 degrees, the complementary angle B will measure 45 degrees as well.

sin(45°) = cos(45°) =$\frac { 1}{\sqrt 2}$
tan(45°) = cot(45°) = 1
sec(45°) = csc(45°) = $\sqrt 2$

Sample Questions

1. If sin(A) = 3/5, find cos(A) and tan(90° – A).

Solution:
Given, sin(A) = 3/5
$cos(A) = \sqrt {(1 – sin^2(A))} = \sqrt {(1 – (3/5)^2)} = 4/5$
tan(90° – A) = cot(A) = cos(A)/sin(A) = (4/5)/(3/5) = 4/3

2. If tan(A) = 7/24, find sin(90° – A) and csc(A).

Solution:
Given, tan(A) = 7/24
$sin(A) = tan(A)/\sqrt {(1 + tan^2(A))} = 7/25$
$sin(90° – A) = cos(A) = \sqrt {(1 – sin^2(A))} =24/25$
csc(A) =1/sin (A) =25/7

I hope you like this article on Trigonometry ratios of complementary angles

Related Articles

Trigonometric ratios of angle A in terms of sin A
Reciprocal of cos function
Trigonometry formula for triangle