how to convert cot inverse to sin, cos, tan, sec, cosec x inverse

We often need to convert inverse of cot to either inverse of cos, sin, tan, sec, cosec x .In this post we will see how to convert cot inverse to sin, cos, tan, sec, cosec x inverse

Inverse of cot to inverse of sin

Case 1
$cot^{-1} x$ and x > 0

Now we can write as

$\theta=cot^{-1} x$
$cot \theta =x$

Now we know that here $\theta \in [0,\pi/2]$, so it is an acute angle

Now it can be written as

$cot \theta =\frac {x}{1} = \frac {base}{perp}$

In Right angle triangle

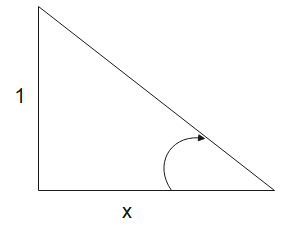
Now then hyp becomes
$\text{hyp} = \sqrt { 1 +x^2}$

So , $sin \theta = \frac {perp}{hyp} = \frac {1}{\sqrt { 1 +x^2}}$

or

$\theta= sin^{-1} \frac {1}{\sqrt { 1 +x^2}}$
or $cot^{-1} x = sin ^{-1} \frac {1}{\sqrt { 1 +x^2}}$

Case 2
$cot^{-1} x$ and x < 0

So value of the function will be in the range $[\pi/2 , \pi)$

Now we know from the property that

$cot^{-1} (-x)= \pi – cot^{-1} (x)$

This can be written as
$cot^{-1} x = \pi – cot^{-1} |x| =\pi – sin ^{-1} \frac {1}{\sqrt { 1 +x^2}}$

This makes sense also as Range of the cot and sin function differ. We can convert with out worrying about the sign in $[0, \pi/2]$ as it is common

Thus ,we have different formula depending on the values of x

Inverse of cot to inverse of cos

Case 1
$cot^{-1} x$ and x > 0

from the above, we can write that

$cos \theta = \frac {base}{hyp} = \frac {x}{\sqrt {1+x^2}}$

or

$cot^{-1} x = cos^{-1} \frac {x}{\sqrt { 1 +x^2}}$

Case 2
$cot^{-1} x$ and x < 0

So value of the function will be in the range $[\pi/2 , \pi)$

Now we know from the property that

$cot^{-1} (-x)= \pi – cot^{-1} (x)$

$cot^{-1} x = \pi – cot^{-1} |x| = \pi – cos^{-1} \frac {|x|}{\sqrt { 1 +|x|^2}}= cos^{-1} \frac {x}{\sqrt { 1 +x^2}}$

So we have same formula for any values of x

$cot^{-1} x = cos^{-1} \frac {x}{\sqrt { 1 +x^2}}$

Inverse of cot to inverse of tan

Case 1
$cot^{-1} x$ and x > 0

from the above, we can write that

$tan \theta = \frac {perp}{base} = \frac {1}{x}$

or

$cot^{-1} x = tan^{-1} \frac {1}{x}$

Case 2
$cot^{-1} x$ and x < 0

Now we know from the property that

$cot^{-1} (-x)= \pi – cot^{-1} (x)$

$cot^{-1} x = \pi – cot^{-1} |x| = \pi – tan^{-1} \frac {1}{|x|}= \pi + tan^{-1} \frac {1}{x}$

This makes sense also as Range of the cot and tan function differ. We can convert with out worrying about the sign in $[0, \pi/2]$ as it is common

Thus ,we have different formula depending on the values of x

Inverse of cot to inverse of sec

Case 1
$cot^{-1} x$ and x > 0

from the above, we can write that

$sec \theta = \frac {hyp}{base} = \frac {\sqrt {1+x^2}}{x}$

or

$cot^{-1} x = sec^{-1} \frac {\sqrt {1+x^2}}{x}$

Case 2
$cot^{-1} x$ and x < 0

So value of the function will be in the range $[\pi/2 , \pi)$

Now we know from the property that

$cot^{-1} (-x)= \pi – cot^{-1} (x)$

$cot^{-1} x = \pi – cot^{-1} |x| = \pi – sec^{-1} \frac {\sqrt {1+x^2}}{|x|}= sec^{-1} \frac {\sqrt {1+x^2}}{x}$

So we have same formula for any values of x

$cot^{-1} x = sec^{-1} \frac {\sqrt {1+x^2}}{x}$

Inverse of cot to inverse of cosec

Case 1
$cot^{-1} x$ and x > 0

from the above, we can write that

$sec \theta = \frac {hyp}{perp} =\sqrt {1+x^2}$

or

$cot^{-1} x = cosec^{-1} \sqrt {1+x^2}$

Case 2
$cot^{-1} x$ and x < 0

So value of the function will be in the range $[\pi/2 , \pi)$

Now we know from the property that

$cot^{-1} (-x)= \pi – cot^{-1} (x)$

$cot^{-1} x = \pi – cot^{-1} |x| = \pi – cosec^{-1} \sqrt {1+x^2}$

I hope you like this article on how to convert cot inverse to sin, cos, tan, sec, cosec x inverse

Related Articles

how to convert cosec inverse to sin, cos, tan, sec x, cot inverse
how to convert sec inverse to sin, cos, tan, cosec x, cot inverse
how to convert sin inverse to cos, tan, sec, cosec x, cot inverse
how to convert cos inverse to sin, tan, cosec x, cot inverse
how to convert tan inverse to sin, cos, sec, cosec x, cot inverse