Trigonometry is an essential branch of mathematics and is included in the CBSE board curriculum. The cosine function is one of the six trigonometric functions and is often used to describe periodic phenomena. In this article, we will provide an overview of cos 2x, its properties, and its applications.
Cos 2x Formula
The formula of cos 2x is given by
$\cos 2x= cos^2 x – sin^2 x$ -(1)
$\cos 2x = 1 – 2 sin^2 x$ -(2)
$\cos 2x= 2 cos^2x – 1$ -(3)
$\cos 2x= \frac {1 – tan^2x }{1 + tan^2 x}$ -(4)
Proof
We know that
$cos (A + B) = cos A cos B – sin A sin B$
Therefore
$\cos 2x= cos (x +x) = cos (x) cos (x) – sin (x) sin (x)= cos^2x – sin^2x$ -(1)
Now we know that sin^2x = 1 -cos^2x
So,
$\cos 2x= cos^2x – sin^2x= cos^2 x – (1-cos^2 x) = 2cos^2 x -1$ – (3)
Now we know that cos^2x = 1 -sin^2x
$\cos 2x= 2cos^2 x -1 = 1 -2 sin^2 x$ – (2)
Now
$\cos 2x= cos^2x – sin^2x = \frac {cos^2x – sin^2x}{1} = \frac {cos^2x – sin^2x}{cos^2x + sin^2 x} $
dividing by $cos^2x$ on numerator and denominator, we get
$\cos 2x= \frac {1 – tan^2x }{1 + tan^2 x}$ -(4)
Derivative of cos 2x
Lets find out the derivative of cos 2x
$\frac {d}{dx} cos 2x =?$
Using chain rule
$\frac {d}{dx} cos 2x =-sin 2x \times 2 = -2 sin 2x$
Another method will be
$\frac {d}{dx} (cos 2x) = \frac {d}{dx} (cos2x – sin2x)$
$= \frac {d}{dx} (cos2x) – \frac {d}{dx} (sin2x)$
$= 2 cos x \times (-sin x) – 2 sin x \times (cos x)$
= -4 cos x sin x
= -2 sin 2x
Graph of Cos 2x
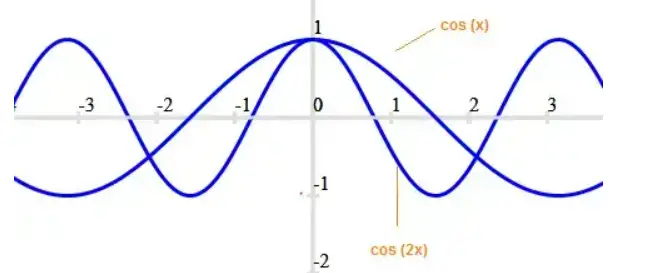
The graph of cos 2x is similar to cos x but graph get shrink
Domain and Range of Cos 2x
Domain and range of cos 2x is same as cos (x)
Domain = $(-\infty, \infty)$
Range = $[-1, 1]$
key properties of cos 2x
- It is a periodic function with a period of $\pi$
- It is an even function, which means that cos 2(-x) = cos 2x.
- Its maximum value is 1, which occurs at x = 0 and x = $\pi$.
- Its minimum value is -1, which occurs at x = $\pi$/2 and x = $3\pi/2$.
