Differentiation of trigonometric functions

Differentiating trigonometric functions is a fundamental concept in calculus. Here’s a quick guide to the derivatives of the basic trigonometric functions. Assume that x is a variable and all functions are differentiable.

Differentiation of Trigonometric Functions

Important formula to find the derivative
$\frac {d}{dx} f(x) =\displaystyle \lim_{h \to 0} \frac {f (x+h) – f(x)}{h}$
$\displaystyle \lim_{x \to 0} \frac {sinx}{x}=1$

Differentiation of Sine Function
$\frac {d}{dx} (sin x) = cos x $
Proof of sin derivative
$\frac {d}{dx} (sin x) = \displaystyle \lim_{h \to 0} \frac {sin (x+h) – sin x}{h}= \displaystyle \lim_{h \to 0} \frac {2cos (\frac {2x+h}{2}) sin \frac {h}{2}}{h}$
$=\displaystyle \lim_{h \to 0} cos (x + \frac {h}{2}) \displaystyle \lim_{h \to 0} \frac {sin \frac {h}{2}}{\frac {h}{2}} = cos x$
as $\displaystyle \lim_{x \to 0} \frac {sinx}{x}=1$

Differentiation of Cos Function
$\frac {d}{dx} (cos x) = -sin x $
Proof
$\frac {d}{dx} (cos x) = \displaystyle \lim_{h \to 0} \frac {cos (x+h) – cos x}{h}= \displaystyle \lim_{h \to 0} -\frac {2sin (\frac {2x+h}{2}) sin \frac {h}{2}}{h}$
$=-\displaystyle \lim_{h \to 0} sin (x + \frac {h}{2}) \displaystyle \lim_{h \to 0} \frac {sin \frac {h}{2}}{\frac {h}{2}} = -sin x$
as $\displaystyle \lim_{x \to 0} \frac {sinx}{x}=1$

Differentiation of Tan Function
$\frac {d}{dx} (tan x) = sec^2x $
Proof
$\frac {d}{dx} (tan x) = \displaystyle \lim_{h \to 0} \frac {tan (x+h) – tan x}{h}= \displaystyle \lim_{h \to 0} \frac {1}{h}[\frac {sin(x+h)}{cos(x+h) }- \frac {sin(x)}{cos(x)}]$
$=\displaystyle \lim_{h \to 0} \frac {1}{h}\frac {sin(x+h)cos (x) – sin(x) cos (x+h)}{cos (x+h) cos x}$
$=\displaystyle \lim_{h \to 0} \frac {1}{h} \frac {sin (x+h -x)}{cos (x+h) cos x} $
$=\displaystyle \lim_{h \to 0} \frac {sin h}{h} \displaystyle \lim_{h \to 0} \frac {1}{cos (x+h) cos x}= sec^2 x$
as $\displaystyle \lim_{x \to 0} \frac {sinx}{x}=1$

Alternatively, since $ \tan(x) = \frac{\sin(x)}{\cos(x)} $, you can use the quotient rule to derive this.

$\frac {d}{dx} [f(x)/g(x)]=\frac {g(x) \frac {d}{dx} f(x) – f(x) \frac {d}{dx} g(x)}{[g(x)]^2} $

$\frac {d}{dx} [sin(x)/cos(x)]=\frac {cos(x) cos(x) – sin(x) (-sin(x))}{[cos(x)]^2} = \frac {1}{[cos(x)]^2}= sec^2 x$

Differentiation of Cot Function
$\frac {d}{dx} (cot x) = -cosec^2x $
Proof

Now $ \cot(x) = \frac{\cos(x)}{\sin(x)} $, and the quotient rule applies.

$\frac {d}{dx} [f(x)/g(x)]=\frac {g(x) \frac {d}{dx} f(x) – f(x) \frac {d}{dx} g(x)}{[g(x)]^2} $

$\frac {d}{dx} [cos(x)/sin(x)]=\frac {sin(x) (-sin(x)) – cos(x) cos(x)}{[sin(x)]^2} = \frac {-1}{[sin(x)]^2}= -cosec^2 x$

Differentiation of Secant Function
$\frac {d}{dx} (sec x) = sec x . tan x $

Proof

Now $\sec (x) = \frac {1}{cos(x)}$ , and the quotient rule applies.

$\frac {d}{dx} [f(x)/g(x)]=\frac {g(x) \frac {d}{dx} f(x) – f(x) \frac {d}{dx} g(x)}{[g(x)]^2} $

$\frac {d}{dx} [1/cos(x)]=\frac {0 + sin(x)}{[cos(x)]^2} = sec x . tan x $

Differentiation of Cosecant Function
$\frac {d}{dx} (cosec x) = -cosec x . cot x$

Proof

Now $cosec (x) = \frac {1}{sin(x)}$ , and the quotient rule applies.

$\frac {d}{dx} [f(x)/g(x)]=\frac {g(x) \frac {d}{dx} f(x) – f(x) \frac {d}{dx} g(x)}{[g(x)]^2} $

$\frac {d}{dx} [1/sin(x)]=\frac {0 – cos(x)}{[sin(x)]^2} = -cosec x . cot x$

Chain Rule for composite Trigonometric Functions

When differentiating composite trigonometric functions, the chain rule is often necessary. For example, if you have a function like $ \sin(2x) $, its derivative is $ 2\cos(2x) $, obtained by applying the chain rule.

Examples

1. Differentiating $ \sin(3x^2) $
   \[ \frac{d}{dx}[\sin(3x^2)] = \cos(3x^2) \cdot 6x \]
   Here, the chain rule is applied: first, differentiate ( \sin(u) ) with respect to ( u ), and then multiply by the derivative of ( u = 3x^2 ) with respect to ( x ).
2. Differentiating $ \tan(x^3) $
   \[ \frac{d}{dx}[\tan(x^3)] = \sec^2(x^3) \cdot 3x^2 \]
   Again, the chain rule is used.

Higher Order Derivatives

For higher-order derivatives, trigonometric functions exhibit cyclic patterns. For instance, the derivatives of sine and cosine functions repeat every four derivatives.

$\frac {d}{dx} sin (x) = cos (x)$
$\frac {d^2}{dx^2} cos (x) = -sin (x)$
$\frac {d^3}{dx^3} (-sin (x)) = -cos (x)$
$\frac {d^4}{dx^4} (-cos (x)) = sin (x)$

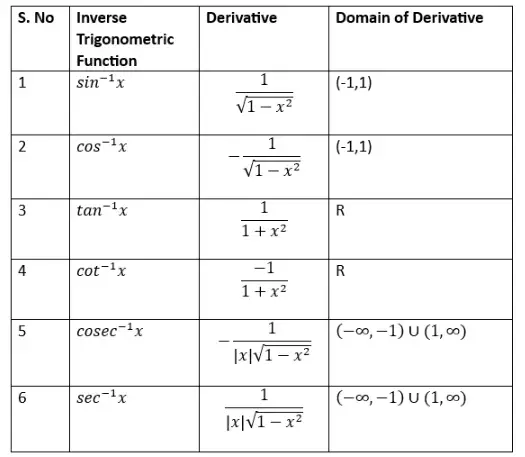
Differentiation of Inverse Trigonometric Functions