how to convert sec inverse to sin, cos, tan, cosec x, cot inverse

We often need to convert inverse of sec to either inverse of cos, sin, tan, cosec , cot .In this post we will see how we can do it easily

Inverse of sec to inverse of sin

Case 1
$sec^{-1} x$ and x > 1

Now we can write as

$\theta=sec^{-1} x$
$sec \theta =x$

Now we know that here $\theta \in [0,\pi/2]$, so it is an acute angle

Now it can be written as

$sec \theta =\frac {x}{1} = \frac {hyp}{base}$

In Right angle triangle

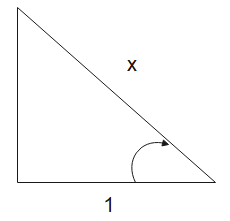
Now then

$perp = \sqrt {x^2 -1}$

Now

$sin \theta = \frac {perp}{hyp} = \frac {\sqrt {x^2 -1}}{x}$

or $sec^{-1}x = sin^{-1} \frac {\sqrt {x^2 -1}}{x}$

Case 2
$sec^{-1} x$ and x < -1

So value of the function will be in the range $(\pi/2 , \pi]$

Now we know from the property that

$sec^{-1} (-x) = \pi – sec^{-1} (x)$

Therefore

$sec^{-1} (x) = \pi – sec^{-1} |x| = \pi – sin^{-1} \frac {\sqrt {x^2 -1}}{|x|} = \pi + sin^{-1} \frac {\sqrt {x^2 -1}}{x}$

This makes sense also as Range of the sec and sin function differ. We can convert with out worrying about the sign in $[0, \pi/2] as it is common

Thus ,we have different formula depending on the values of x

Inverse of sec to inverse of cos

This is by property

$sec^{-1} x = cos^{-1} \frac {1}{x}$

Inverse of sec to inverse of tan

Case 1
$sec^{-1} x$ and x > 1

$tan \theta = \frac {perp}{base} = \sqrt { x^2 -1}$
so $sec^{-1} x = tan^{-1} \sqrt { x^2 -1}$

Case 2

$sec^{-1} x$ and x < -1

Now we know from the property that

$sec^{-1} (-x) = \pi – sec^{-1} (x)$

Therefore

$sec^{-1} (x) = \pi – sec^{-1} |x| = \pi – tan^{-1} \sqrt {x^2 -1} $

This makes sense also as Range of the sec and sin function differ. We can convert with out worrying about the sign in $[0, \pi/2] as it is common

Thus ,we have different formula depending on the values of x

Inverse of sec to inverse of cosec

Case 1
$sec^{-1} x$ and x > 1

$cosec \theta = \frac {hyp}{perp} = \frac {x}{\sqrt { x^2 -1}}$
so $sec^{-1} x = cosec^{-1} \frac {x}{\sqrt { x^2 -1}}$

Case 2

$sec^{-1} x$ and x < -1

Now we know from the property that

$sec^{-1} (-x) = \pi – sec^{-1} (x)$

Therefore

$sec^{-1} (x) = \pi – sec^{-1} |x| = \pi – cosec^{-1} \frac {|x|}{\sqrt { x^2 -1}}= \pi + cosec^{-1} \frac {x}{\sqrt { x^2 -1}} $

This makes sense also as Range of the sec and sin function differ. We can convert with out worrying about the sign in $[0, \pi/2] as it is common

Thus ,we have different formula depending on the values of x

Inverse of sec to inverse of cot

Case 1
$sec^{-1} x$ and x > 1

$cot \theta = \frac {base}{perp} = \frac {1}{\sqrt { x^2 -1}}$
so $sec^{-1} x = cot^{-1} \frac {1}{\sqrt { x^2 -1}}$

Case 2

$sec^{-1} x$ and x < -1

Now we know from the property that

$sec^{-1} (-x) = \pi – sec^{-1} (x)$

Therefore

$sec^{-1} (x) = \pi – sec^{-1} |x| = \pi – cot^{-1} \frac {1}{\sqrt { x^2 -1}} $

This makes sense also as Range of the sec and sin function differ. We can convert with out worrying about the sign in $[0, \pi/2] as it is common

Thus ,we have different formula depending on the values of x