In this post, we will checking how to prove a function is one-to-one graphically .Examples and Problems are also given to help the student. This will also answer the question How do you know if the function is one-one
how to prove a function is one-to-one graphically
We can prove using Horizontal line test.
What is horizontal line test
A function is one one if, and only if, for all elements a1 and a2 in A,
if f(a1) = f(a2), then a1 = a2
On the graph, two points will lie in the same horizontal line if and only if the second coordinate of the two points is the same. i,e we have the condition where
f(a1) = f(a2) and a1 is not equal to a2
Therefore if a horizontal line intersects the graph at two points then it is not an one-one function. This is called the Horizontal line test. If all horizontal lines intersect a curve at most once then the curve represents a one-one function.
How to use the it
To use it, take a rule or other straight edge and draw a line parallel to the x-axis for any chosen value of y. If the horizontal line you drew intersects the graph more than once for any value of y then the graph is not the graph of a one-one function. If alternatively, a horizontal line intersects the graph no more than once, no matter where the horizontal line is placed, then the graph is the graph of a one one function.
Examples
(a) $f(x) = x^2$
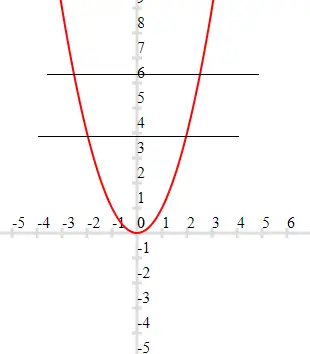
Clearly this is not one-one function
(b) $f(x) = x+3$
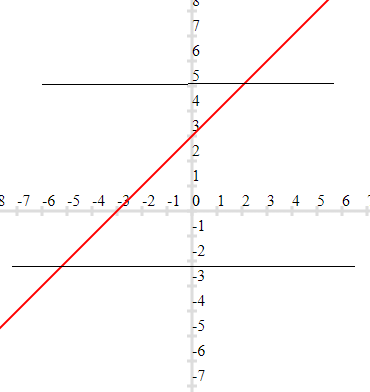
Clearly this is one-one
(c) $f(x) = x|x|$
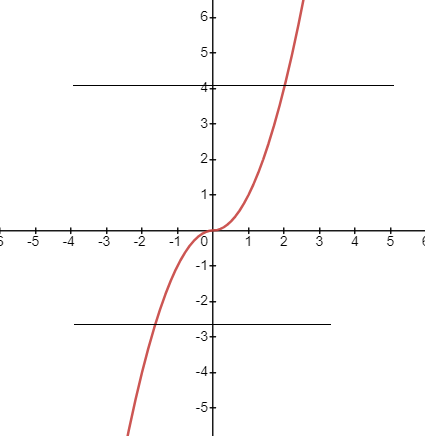
Clearly this is one-one
