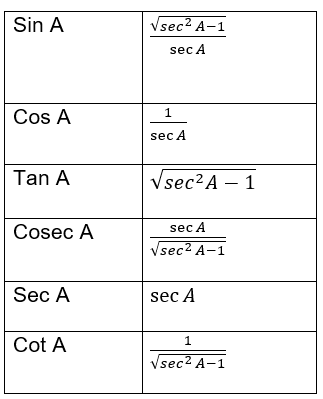
In this post ,we will see how we can write all the Trigonometric ratios of angle A in the terms of sec A. Here we would be focusing on acute angle A only
Value of Cos A in terms of sec A
$cos A = \frac {1}{sec A}$
Value of Sin A in terms of sec A
From Trigonometric Identity
$\sin ^2 A + \cos ^2 A= 1$
or
$\sin ^2 A = 1- \cos ^2 A$
$\sin A = \sqrt { 1 – \cos ^2 A} = \sqrt { 1- \frac {1}{sec^2 A}}= \frac {\sqrt {sec^2 A -1}}{sec A}$
Value of tan A in terms of sec A
Now Value of tan is given by
$tan A = \frac { \sin A}{\cos A} = \sqrt {sec^2 A -1}$
Value of cosec A in terms of sin A
Now Value of cosec is given by
$\csc A = \frac {1}{\sin A} = \frac { sec A}{\sqrt {sec^2 A -1}}$
Value of cot A in terms of sin A
$\cot A = \frac {1}{\tan A} = \frac {1}{\sqrt {sec ^2 A- 1}}$
In short