For any triangle , we have following formula involving trigonometric ratios.
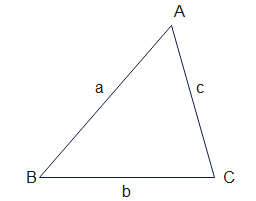
Trigonometry formula for triangle
Formula 1
$\frac {sin A}{a} = \frac {sin B}{c} = \frac {sin C}{c}$
Formula 2
$cos A = \frac {b^2 + c^2 -a^2}{2bc}$
$cos B = \frac {a^2 + c^2 -b^2}{2ac}$
$cos C = \frac {a^2 + b^2 -c^2}{2ab}$
Formula 3
Area of the triangle is given by
$S= \sqrt {s(s-a)(s-b)(s-c)} = \frac {1}{2} bc sin A =\frac {1}{2} ac sin B = \frac {1}{2} ab sin C$
where $s= \frac {a+b+c}{2}$
Formula 4
The below formula is deduced from above only
$sin A= \frac {2}{bc} \sqrt {s(s-a)(s-b)(s-c)} $
$sin B= \frac {2}{ac} \sqrt {s(s-a)(s-b)(s-c)} $
$sin C= \frac {2}{ab} \sqrt {s(s-a)(s-b)(s-c)} $
Formula 5
The Radius of the circumcenter of the triangle is given by
$R =\frac {abc}{4S}$
where S is the area of the triangle
We can write this in trigonometric relation as
$R= \frac {a}{2 sin A} = \frac {b}{2 sin B}= \frac {c}{2 sin C}= \frac {abc}{4S}$
Formula 6
a=b cos C + c Cos B
b=aCos C + c Cos A
c= aCos B + b Cos A
Formula 7
The Radius of the incenter of the triangle is given by
$r= \frac {S}{s]}$
where S is the area of the triangle
and $s = \frac {a+b+c}{2}$
We can write this in trigonometric relation as
$r=(s-a) tan \frac {A}{2} = (s-b) tan \frac {B}{2}= (s-c) tan \frac {C}{2}$
$r=4R sin \frac {A}{2} sin \frac {B}{2} sin \frac {C}{2}$
Formula 8
$sin \frac {A}{2} = \sqrt { \frac {(s-b)(s-c}{bc}}$
$sin \frac {B}{2} = \sqrt { \frac {(s-a)(s-c}{ac}}$
$sin \frac {C}{2} = \sqrt { \frac {(s-a)(s-b}{ab}}$
