The cosine function, often denoted as cos(x), is a fundamental trigonometric function with a wide range of applications in mathematics, physics, and engineering. In this article, we will specifically discuss the value of the cosine function when its argument is zero, or cos(0), and its significance in various domains.
Value of Cos 0
Value of cos 0 is 1.
Lets see the unit circle method on how to calculate it
The Cosine Function and the Unit Circle
The cosine function can be defined in several ways, but one common approach is to use the unit circle – a circle with a radius of one centered at the origin of the coordinate plane. Any angle in standard position (vertex at the origin and initial side along the positive x-axis) can be associated with a point on the unit circle. The cosine of an angle is defined as the x-coordinate of this point.
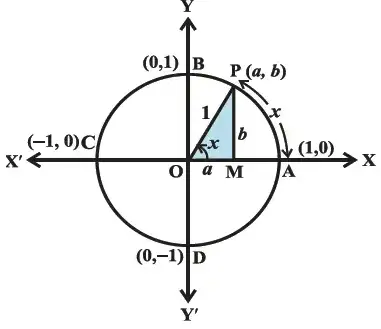
Cos x =a
When the angle is zero (0), the point on the unit circle associated with this angle is (1, 0), as it lies on the positive x-axis. Since the cosine function represents the x-coordinate of this point, we can conclude that
cos(0) = 1.
How to find Cos 0 using other method
Method 1
We know that
Cos^2 x + sin^2 x =1
Now when x=0
$cos^2 0 + sin^2 0 =1$
now we know that sin 0 =0
Therefore
Cos 0 =1
Method 2
angle sum formula
The angle sum formula for cosine states that
cos(a + b) = cos(a)cos(b) – sin(a)sin(b).
Setting a = 0, we obtain
cos(b) = cos(0)cos(b) – sin(0)sin(b)
cos(b) = cos(0)cos(b)
cos(0) = 1.
Applications of Cos 0
The value of cos(0) = 1 has practical implications in various fields:
- In physics, it is useful when calculating the work done by a force or the dot product of two vectors, as the cosine of the angle between them plays a crucial role.
- In signal processing, the cosine function is used to model periodic signals, and the value of cos(0) is relevant in understanding phase shifts and waveform characteristics.
- In mathematics, the value of cos(0) plays a key role in the analysis of trigonometric functions, the study of Fourier series, and the solution of differential equations.
Sample Questions
Example 1
