Area of quadrant of a circle

TL;DR
The area of a quadrant equals one-quarter of the circle’s total area and uses the formula: Area = ?r²/4, with r representing the circle’s radius. Since each quadrant covers exactly 25% of the complete circle, this calculation divides the full circle area by four. For instance, when a circle has an 8 cm radius, the quadrant area becomes (? × 8²)/4 = 16? cm².

Quadrant of a Circle

A quadrant is one of four equal parts of a circle. Imagine drawing two lines across the circle: one horizontal and one vertical, both passing right through the centre, and making a perfect right angle (90 degrees) between them. These lines divide the circle into four equal sections called quadrants.

Each quadrant represents one-fourth of the entire circle. So, the area of a quadrant is one-fourth the area of the whole circle.

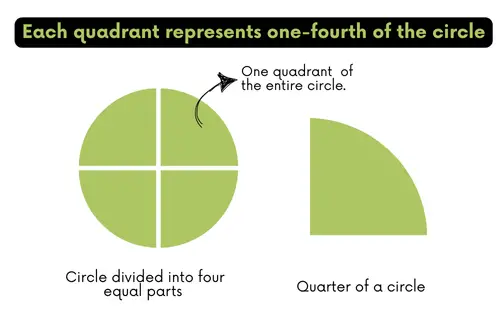
All four quadrants have identical areas and shapes, making each one exactly 25% of the complete circle.

Area of a Circle Recap

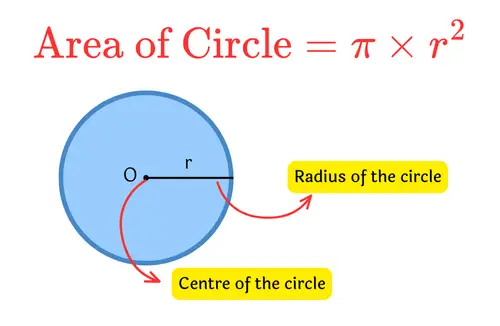
Before finding the area of a quadrant, we should know how to find the area of the full circle. The formula for the area of a circle is:
$$
\text{Area of Circle} = \pi \times r^2
$$

Here, $r$ is the radius — the distance from the centre of the circle to any point on its edge. The symbol $\pi$ (pi) is a constant approximately equal to 3.1416.

Finding the Area of a Quadrant

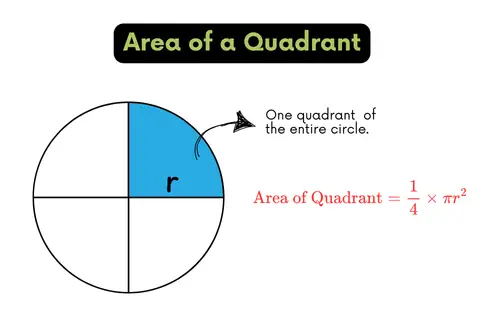
Since a quadrant is exactly one-fourth of the circle, its area is:
$$
\text{Area of Quadrant} = \frac{1}{4} \times \pi r^2
$$
This means to find the area of a quadrant, we calculate the whole circle’s area first, and then divide it by 4.

Step-by-step process:

1. Find or measure the radius $r$.
2. Calculate the area of the whole circle using the formula $\pi r^2$.
3. Divide that area by 4 to get the area of the quadrant.
4. Write the answer with square units (such as cm², m², inch²).

Example 1: Area of a Quadrant with Radius 6 cm

If the radius of the circle is 6 cm:

• The area of the circle is $\pi \times 6^2 = \pi \times 36 = 36\pi \text{ cm}^2$.
• Area of the quadrant = $\frac{1}{4} \times 36\pi = 9\pi \text{ cm}^2$.

Approximating $\pi$ as 3.14, the area equals about $9 \times 3.14 = 28.26 \text{ cm}^2$.

Example 2: Finding Radius from Quadrant Area

Suppose the area of a quadrant is $16\pi \text{ cm}^2$. To find the radius:

• Use $\frac{1}{4} \pi r^2 = 16 \pi$.
• Divide both sides by $\pi$: $\frac{1}{4} r^2 = 16$.
• Multiply both sides by 4: $r^2 = 64$.
• Take the square root: $r = 8 \text{ cm}$.

So, the radius is 8 cm.

Additional Notes on Diameter and Circumference

The diameter $d$ is twice the radius: $d = 2r$. The formula for the area of a quadrant can be rewritten in terms of diameter:
$$
\text{Area of Quadrant} = \frac{1}{16} \pi d^2
$$
If given circumference $C = 2 \pi r$, solve for radius:
$$
r = \frac{C}{2\pi}
$$
and then use this radius in the quadrant area formula.

Area of quadrant of a circle calculator