Case study class 10 Maths Questions

Why Case study questions are important

• Case study questions in Class 10 Maths are designed to assess students’ understanding and application of mathematical concepts in real-world scenarios. These questions require students to analyze a given situation, identify relevant mathematical principles, and apply them to solve the problem at hand.
• Case study questions help to foster critical thinking, problem-solving skills, and the ability to connect mathematical concepts with practical situations.
• These questions involve multiple mathematical topics such as geometry, algebra, statistics, probability, and more.

Case study class 10 Maths Questions

Here are some of the Case study class 10 Maths Questions

Question 1

A test consists of ‘True’ or ‘False’ questions. One mark is awarded for every correct answer while ¼ mark is deducted for every wrong answer. A student knew answers to some of the questions. Rest of the questions he attempted by guessing. He answered 120 questions and got 90 marks.

1. If answer to all questions he attempted by guessing were wrong, then how many questions did he answer correctly?
2. How many questions did he guess?
3. If answer to all questions he attempted by guessing were wrong and answered 80 correctly, then how many marks he got?
4. If answer to all questions he attempted by guessing were wrong, then how many questions answered correctly to score 95 marks?

Answer

Let the no of questions whose answer is known to the student x and questions attempted by cheating be y
x + y =120
x-1/4y =90
solving these two
x=96 and y= 24

1. He answered 96 questions correctly.
2. He attempted 24 questions by guessing.
3. Marks = 80- ¼ 0f 40 =70
4. x – ¼ 0f (120-x) =95
   5x=500, x = 100

Question 2

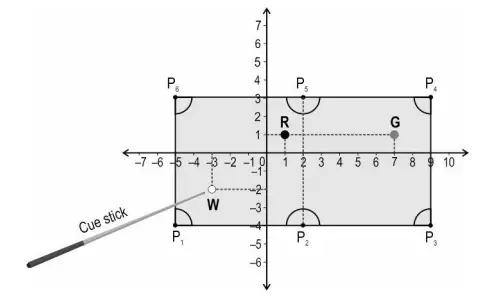
The snooker table has six pockets (P1, P2, P3, P4, P5 and P6) and he has shown three balls – white (W), red (R) and green (G) on the table. The objective of the game is to use the white ball to hit the coloured balls into the pockets using a cue stick.
(i) How much distance will a ray travel if sent from the green ball to the nearest pocket? Show your work.
(ii) Riju wants to place a yellow ball at the midpoint of the line connecting the white and green balls.
Find the coordinates of the point at which he should place the yellow ball. Show your steps.
(iii) Riju is running a trial on his game. He struck the white ball in a way that it rebound off the rail (line connecting P4 and P6) and went into the pocket P2.
After the rebound, the ball crossed the x-axis at point X( 2/7, 0) on the way to the pocket.
The ratio of the distance between the rail and point X and the distance between point X and the pocket was 3:4.
Find the coordinates of the point at which the ball struck the rail. Show your steps.
(iv) Riju wants to hit a blue ball placed at (-1, -3) into pocket P5 along a straight path. Would the red ball lie on the straight path between the blue ball and P5? Justify your answer.

Answer

(i) Identifies the coordinates of the green ball as (7, 1) and the nearest pocket P4 as (9, 3). Using the distance formula we can calculate the distance . The distance $\sqrt 8$ or $2 \sqrt 2$ units
(ii) The coordinates of the yellow ball using the midpoint formula with W(-3, -2) and G(7, 1) will be ( 2, -1/2)
(iii) Lets Considers the point where the ball struck the rail as (c, 3) and the coordinates of P2 (other end point) as (2, -4). Now we can find c using the section formula

$\frac {2}{7} = \frac {4c+6}{7}$ or c=-1
So the point is (-1,3)
(iv) The distance between the blue ball and red ball (BR) using distance formula is $2 \sqrt 5$
The distance between the red ball and P5 (RP5) using distance formula is $\sqrt 5$ units
The distance between the blue ball and P5 (BP5) using distance formula is $3 \sqrt 5$ unit
It Concludes that red ball will lie on the straight path between the blue ball and P5 by proving that the three points are collinear as BR + RP5 = BP5.

Question 3

The figure given alongside shows the path of a diver, when she takes a jump from the diving board. Clearly it is a parabola.
Annie was standing on a diving board, 48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time‘t’ in seconds is given by the polynomial h(t) such that

$h(t)=-16t^2+ 8t + p$.

(i) What is the value of p?
(a) 0
(b) – 48
(c) 48
(d) 48/-16

(ii)At what time will she touch the water in the pool?
(a) 30 seconds
(b) 2 seconds
(c) 1.5 seconds
(d) 0.5 seconds

(iii) Rita’s height (in feet) above the water level is given by another polynomial p(t) with zeroes -1 and 2. Then p(t) is given by-
(a) t² + t – 2.
(b) t² + 2t – 1
(c) 24t² – 24t + 48.
(d) -24t² + 24t + 48.

(iv) A polynomial q(t) with sum of zeroes as 1 and the product as -6 is modelling Anu’s height in feet above the water at any time t( in seconds). Then q(t) is given by
(a) t² + t + 6
(b) t² + t -6
(c) -8t² + 8t + 48
(d) 8t² – 8t + 48

(v) The zeroes of the polynomial r(t) = -12t² + (k-3)t +48 are negative of each other. Then k is
(a) 3
(b) 0
(c) -1.5
(d) -3

Answer

(i) c
(ii) b
(iii) d
(iv) c
(v) a

Question 4

Your friend Veer wants to participate in a 200m race. He can currently run that distance in 51 seconds and with each day of practice it takes him 2 seconds less. He wants to do in 31 seconds .

1. Which of the following terms are in AP for the given situation
   a) 51,53,55….
   b) 51, 49, 47….
   c) -51, -53, -55….
   d) 51, 55, 59…
2. What is the minimum number of days he needs to practice till his goal is
   achieved
   a) 10
   b) 12
   c) 11
   d) 9
3. Which of the following term is not in the AP of the above given situation
   a) 41
   b) 30
   c) 37
   d) 39
4. If nth term of an AP is given by $a_n = 2n + 3$ then common difference of an AP is
   a) 2
   b) 3
   c) 5
   d) 1
5. The value of x, for which 2x, x+ 10, 3x + 2 are three consecutive terms of an
   AP
   a) 6
   b) -6
   c) 18
   d) -18

Answer

1. b
2. c
3. b
4. a
5. a

Question 5

In given figure, a circle with Centre O is inscribed in a triangle ABC, such that it touches the sides AB, BC and CA at points D, E
and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively

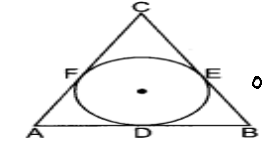
1. Find the length of AD
   a) 7
   b) 8
   c) 5
   d) 9
2. Find the Length of BE
   a) 8
   b) 5
   c) 2
   d) 9
3. Find the length of CF
   a) 9
   b) 5
   c) 2
   d) 3
4. If radius of the circle is 4cm, Find the area of ?OAB
   a) 20
   b) 36
   c) 24
   d) 48
5. Find area of triangle ABC
   a) 50
   b) 60
   c) 100
   d) 90

Answer

1. a) 7
2. b) 5
3. d) 3
4. c) 24
5. b) 60

Question 6

The vertices of a triangle are A(1, 2), B(5, 6), and C(-3, 4).

1.The length of side AB is

(a) $4 \sqrt 2$
(b) $2 \sqrt 5$
(c) $2 \sqrt 17$
(d) $2 \sqrt 2$

2. The centroid of the triangle

(a) (1,4)
(b) (-1,4)
(c) (2,2)
(d) (1 ,-4)

3. it is an
(a)equilateral triangle.
(b) isosceles triangle.
(c) scalene triangle.

Answer
1. (a)
2. (a)
3. (c)

Question 7

A bag contains 5 red balls, 4 blue balls, and 6 green balls. If a ball is drawn randomly, find the probability of getting:

1.A red ball

(a)1/2
(b)1/3
(c) 1/13
(d) 2/5

2.A blue or green ball

(a)1/2
(b)1/3
(c) 2/3
(d) 2/5

3.A green ball on the second draw, given that the first ball drawn was red

(a)3/7
(b)1/3
(c) 1/13
(d) 2/5

Answers

1. (b)
2. (c)
3. (a)

Question 8

One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.

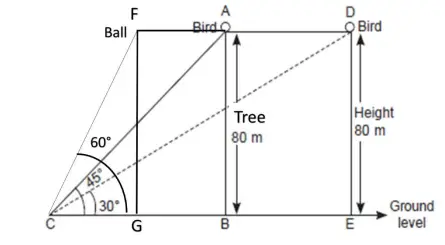
1.At what distance from the foot of the tree was he observing the bird sitting on the tree?

(a) 80 m
(b) 60 m
(c) $80 \sqrt 3$ m
(d) None of these

2.How far did the bird fly in the mentioned time?

(a) 80 m
(b) $80 \sqrt 3$ m
(c) $80 ( \sqrt 3 -1)$ m
(d) None of these

3.After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball?

(a) 80 m
(b) $80 \sqrt 3$ m
(c) $80 ( \sqrt 3 -1)$ m
(d) $80 (1 – \frac {1}{\sqrt 3})$ m

4.What is the speed of the bird in m/min if it had flown $20( \sqrt 3 + 1)$ m?

(a) 600 m/s
(b) $600 (\sqrt 3 +1)$ m/s
(c) $600 ( \sqrt 3 -1)$ m/s
(d) $600 (1 – \frac {1}{\sqrt 3})$ m/s

Answer

1. (a)
2. (c)
3. (d)
4. (b)

Related Articles

CBSE Class 10th maths important questions
Class 10 Maths