Denominator and Divisor

In the study of mathematics, particularly in fractions and division operations, two terms that often arise are denominator and divisor. Let’s explore both concepts in detail.

What is Denominator?

Definition: In a fraction, the denominator represents the total number of equal parts into which a quantity is divided. It is the number below the line in a fractional expression.

Example of Denominator

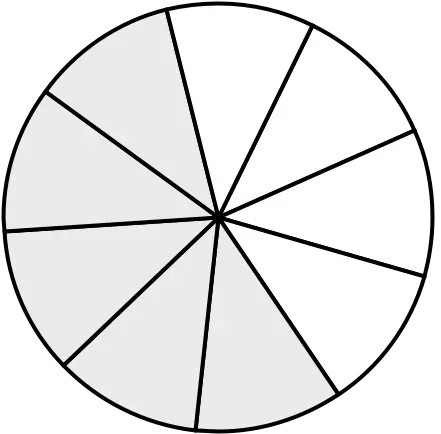
In the fraction \(\frac{5}{8}\), the number 8 is the denominator. This means that the whole is divided into 8 equal parts, and the fraction represents 5 of those parts.

The diagram given below illustrates this. It shows a circle and divides it into 8 equal parts. Five shaded parts represent the fraction \(\frac{5}{8}\).

Questions:

1. What is the denominator in the fraction \(\frac{3}{4}\)?
2. How does the value of the denominator affect the value of the fraction?

Answers:

1. In the fraction \(\frac{3}{4}\), the denominator is 4.
2. The larger the denominator, the smaller each part of the whole, and therefore the smaller the value of the fraction (assuming the numerator remains constant).

2. Divisor

Definition: In a division operation, the divisor is the number by which another number (called the dividend) is divided.

Example of Divisor

In the division operation \(\frac{20}{4} = 5\), the number 4 is the divisor. It represents how many times the dividend (20) is to be divided.

The diagram above shows an example of a divisor by drawing 20 dots and dividing them into groups of four. There will be five groups to demonstrate that 20 divided by four equals five.

Questions:

1. What is the divisor in the division operation \(\frac{15}{3} = 5\)?
2. What happens to the quotient if the divisor is increased?

Answers:

1. In the division operation \(\frac{15}{3} = 5\), the divisor is 3.
2. If the divisor is increased, the quotient (result of division) decreases, provided the dividend remains the same.

Comparison Between Denominator and Divisor

While the denominator and divisor are both related to division, they serve different roles. The denominator tells us into how many equal parts a whole is divided in the context of fractions, while the divisor tells us by what number we are dividing another number in the context of a division operation.

The difference between the denominator and the divisor can be clearly illustrated in the form of a table.

Attribute	Denominator	Divisor
Definition	Number of equal parts in a fraction.	Number by which another number is divided.
Context	Used in a fraction (e.g. \( \frac{a}{b} \)).	Used in a division operation (e.g. \( \frac{a}{b} = c \)).
Position	Found below the line in a fraction.	Used as the ‘dividing by’ number in a division expression.
Effect on Value	The larger the denominator, the smaller the value of the fraction (for a fixed numerator).	The larger the divisor, the smaller the quotient (for a fixed dividend).
Example	In \( \frac{5}{8} \), 8 is the denominator.	In \( \frac{20}{4} = 5 \), 4 is the divisor.
Diagram	Can be represented by dividing a shape into equal parts.	Can be represented by grouping objects into equal sets.

Questions for Reflection:

1. How is the role of the denominator in a fraction different from the role of the divisor in a division operation?
2. Can you think of a mathematical expression where both the concepts of the denominator and divisor are present?

Answers:

1. The denominator divides a whole into equal parts in a fraction, whereas the divisor divides one number by another in a division operation.
2. In the expression \(\frac{\frac{15}{3}}{5}\), 3 is the denominator of the fraction and 5 is the divisor in the overall division.

Denominator and Divisor