Number 63 is a composite number and we will find how to find the factors of 63. We will also see techniques to find out the Prime factorisation of 63 easily
Factors of 63
A factor of a number is an exact divisor of that number. So factors of 63 are the numbers which are exact divisors of 63.
Factors of any number can be found by finding the number which divides the number without remainder, or alternatively, numbers that can multiply together to equal the target number being converted
Let us check how to find the factors
Method -1
Factors can be found by finding the numbers that when multiplied together give the number 63. Now to find the numbers we can start with the integer 1 and keep increasing it by 1 and we will discard where the other number cannot be found. We will stop at a point where we start seeing the repetition of numbers We will find the multiplication one by one and start writing it down. So
$63 = 1 \times 63$
$63= 3 \times 21 $
$63 = 7 \times 9 $
$63 = 9 \times 7 $
We can stop here as 9 and 7 have occurred earlier.
So factors are 1,63,3,21,7,9
Putting the factors in ascending order, we get
1,3,7,9,21,63
Method -2
Factors can be found by finding the numbers which divide the number without a remainder. We can start with the following sequence: 1,2,3,4… and go till the mid-point of that number.
$63/3 = 21$ . No Remainder
$63/7 = 9$. No remainder
$63/9=7$. No remainder.
$63/21=3 $. No remainder.
So factors are 1,3,7, 9,21,63
Hence Factors of 63 are 1,3,7,9,21,63
prime factorization of 63
When a number is expressed as a product of its factors we say that the number has been factorized. When the factorization contains the prime number only then it is called prime factorization.
Now let us look at how to find the prime factorization
There are two methods that can be used.
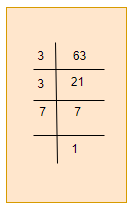
Division method
We divide the number 36 by 2, 3,4,5,6,7, etc. in this order repeatedly so long as the quotient is divisible by that number.
Thus, the prime factorization is $3 \times 3 \times 7$ or $3^2 \times 7$
Factor Tree Method
In this method, we first think about any two factors, and then we think about two factors of respective numbers. This goes till the factors are prime.
We can have many factor trees depending on the starting point but all of them will show the same prime factors.
Let’s check the different Factor trees for number 63
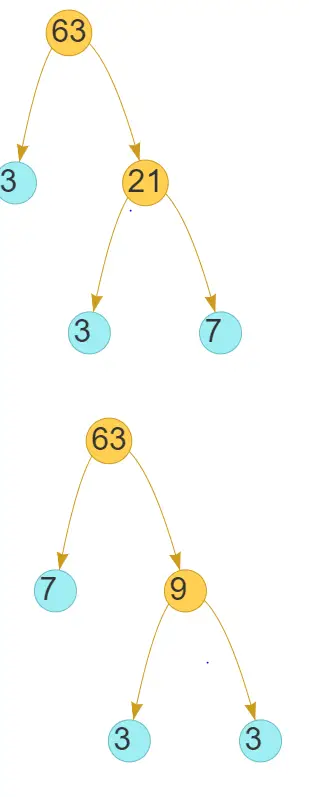
Hence the Prime Factorization is $3^2 \times 7$
Factors of 63 in pair
We can find the factors of number 63 in pairs, by multiplying two numbers in a pair to get the original number as 36, such as:
$63 = 1 \times 63$
$36 = 3 \times 21 $
$36 = 7 \times 9$
So factor in pair are (1,63) , (3,21) ,(7,9)
Hope you like the post
Also Reads
prime factorization of 100
Table of Factors
factors of 35
 Skip to content
Skip to content