Horizontal projectile motion : Derivation and formula

Horizontally launched projectile

concept, formula, and derivation

In this article, we will learn about horizontal projectile motion. In this case, the projectile is launched or fired parallel to horizontal. So, it starts with a horizontal initial velocity, some height ‘h’ and no vertical velocity. I am assuming that you know about the basic concepts of projectile motion.

Projectile motion is a form of motion in which an object or particle (called a projectile) is thrown with some initial velocity near the earth’s surface, and it moves along a curved path under the action of gravity alone.

For the derivation of various formulas for horizontal projectile motion, consider the figure given below,

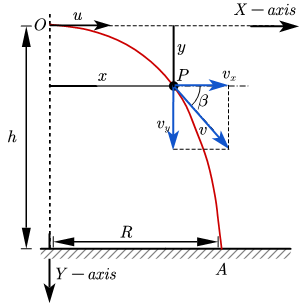
Suppose a body is thrown horizontally from a point \(O\) with velocity \(u\). Point \(O\) is at height \(h\) above the ground.
Now the body has two simultaneously independent motions.
(i) motion with uniform horizontal velocity \(u\).
(ii) vertically downward accelerated motion with constant acceleration \(g\).
A body moves along path \(OPA\) under the influence of these two independent motions.

Trajectory of the projectile

After a time t suppose the body reaches point \(P\left( x,y \right)\) then,
Along horizontal axis at
\(u_x = u\) (since motion is with uniform horizontal velocity)
\(a_x = 0\)
\(s_x=x\)
\(distance = speed \times time\) or, \(x = u\times \,t\)
\[t = \frac{x}{u} \tag{1}\]
Along vertical axis ,
\(u_y = 0 \) at time \(t=0\)
\(a_y = g\)
\(s_y = y\)
By second equation of motion,
\begin{align*}
&s_y = u_yt + \frac{1}{2} a_yt^2\\
&\text{Using equation (1) } \text{and putting} u_y = 0 \text{at time} t=0 \\
&y = \text{0 }+ \frac{1}{2} g \left( \frac{x}{u} \right) ^2\\
&y = \frac{1}{2} g \frac{x^2}{u^2}\\
&y = \frac{g x^2}{\text{2 }u^2}
\end{align*}
This is the equation of parabola. So, the trajectory of the projectile fired parallel to the horizontal is a parabola.

The velocity of the projectile at any time

Along the horizontal axis,
\(a_x = 0\)
so, velocity remains constant and velocity at \(A\) along horizontal will also be \(u\).
Along vertical,
\(u_y = 0\)
\(a_y = g\)
By first equation of motion
\(v_y = u_y + a_yt\)
\(v_y = 0 + gt\)
\(v_y = gt\)
Magnitude of resultant velocity at any point \(P\)
\begin{align*}
&v^2 = v_x^2 + v_y^2 \\
&v= \sqrt{u_x^2 + g^2t^2}\end{align*}
Now \(\beta\) is the angle which resultant velocity makes with the horizontal, then
\[\tan \beta =\frac{ v_y^2}{v_x^2\,}=\frac{gt}{u}\]
or,
\[\beta =\tan ^{-1}\left( \frac{gt}{u} \right) \]

Time of flight

It is the total time for which the projectile remains in flight (from \(O\) to \(A\)). Let \(T\) be the time of flight. For vertical downward motion of the body we use \begin{align*}
&s_y = u_gt + \frac{1}{2} a_yt^2\\
&\text{or,}\\
&h=0\times T +\frac{1}{2}gT^2\\
&\text{or,}\\
&T=\sqrt{\frac{2h}{g}}
\end{align*}

Horizontal Range

It is the horizontal distance covered by projectile during the time of flight. It is equal to \(OA=R\). So, \begin{align*}
R&=\text{Horizontal velocity} \times \text{Time of flight}\\
&=u\times T = u\sqrt{\frac{2h}{g}}
\end{align*}So,\[R=u\sqrt{\frac{2h}{g}}\]

Related Articles and links

1. Range of projectile formula derivation
2. projectile motion PHET Simulation