Into functions are those functions where range is a subset of the codomain of the functions but range is not equal to co-domain
Definition
A function f: A-> B is said to be into if every element of B is not image of some element of A under f, i,e
for every y ? B, there does exists a element x in A where $f(x) \ne y$
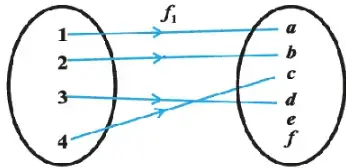
Now we know that A function f: A-> B is said to be onto(surjective) if every element of B is the image of some element of A under f.
So it means a function which is not onto is a into function
Examples
The Greatest integer function
f : R -> R f(x) = [x], rounds a real number x down to the nearest integer.
For example, f(3.8)=[3.8] = 3, f(-2.4)=[-2.4] = -3, and $f(\pi)=[\pi] = 3$
The graph of the function is
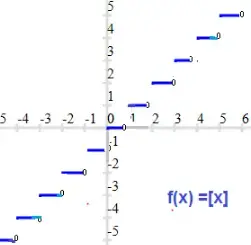
We can see that all the values of codomain does not have the preimage in domain
The absolute value function:
f: R -> R f(x) = |x|
For example, f(3) =|3| = 3, f(2)=|-2| = 2, and |0| = 0.
The graph of the function is
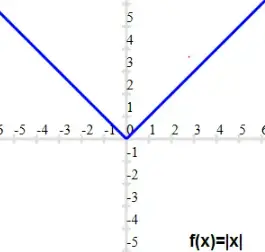
We can see that all the values of codomain does not have the preimage in domain
Square function
$f(x) =x^2$
for example $f(1) =1^2=1$ , $f(-1)= (-1)^2 = 1$
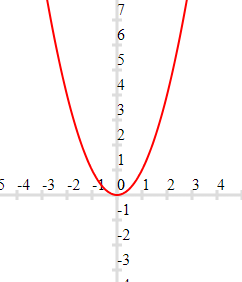
We can see that all the values of codomain does not have the preimage in domain
Difference between into functions and onto functions

Related Articles
