JEE advanced physics questions

Question 1
A ball of mass 100 g is projected vertically upwards from the ground with a velocity of 49 m/s. At the same time, other identical ball is dropped from a height of 98 m to fall freely along the same path as followed by the first ball. After some time two balls collide and stick together and finally fall together. Find the time of flight of the masses.

Solution
We will first find where and when the two balls collide. Let us assume that the balls collide at time t after they have been set into motion. At this instant t when two balls collide, they are at the same height h from the ground as shown below in the figure.

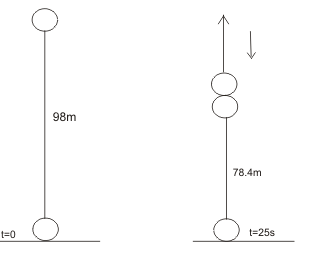
The height of the first ball after t seconds = $49t-0.5(9.8t^2) = 4.9t(20-t)$
Height of second ball after t seconds = 98 – downwards distance moved by it in t seconds
$=98-0.5t^2=4.9(20-t^2)$
Therefore,
$4.9t(20-t)=4.9(20-t^2)$
or
$10t-t^2=20-t^2$
or t=2s

The ball thus collides 2s after the start of their motion.
Their velocities at this instance are
ball 1 : $v_1= (49-9.8 \times 2) \ m/s = 29.4$ m/s directed upwards
ball 2 : $v_2=(0+9.8 \times 2) \ m/s = 19.6$ m/s directed downwards
If v is the velocity of the combined mass of two balls after they stick together due to their collision then from law of conservation of momentum
$200 \times v=100 \times 29.4-100 \times 19.6$
v=4.9 m/s

The joint mass thus moves upwards, after collision with a velocity of 4.9 m/s. Its height above the ground at this instant is (consider the position of either of the balls)
$(98-0.5 \times 9.8 \times 22)=78.4$
We can now find the time t’ taken by this joined mass of the balls to reach the ground. For this joined mass we have
u=4.9 m/s , s=78.4 m , $a=-g = -9.8 \ m/s^2$
$-78.4=4.9t’+0.5(-9.8)t^2$
$t’^2-t’-16=0$
Solving the equation for t’ using formula for quadratic equations and leaving out the negative solution, we get t’=4.532 s
The joint mass thus takes 4.53 s to fall to the ground. Since the balls collide 2 s after they started their motion , the total time of flight is (2+4.53) s = 6.53 s

Question 2
The motion of a particle in XY plane is given by
$x=25+6t^2$
$y=-50-20t+8t^2$
(i)Find the coordinates at t=0?
(ii)Find the velocity at t=0
(iii)Find the acceleration at t=0

Solution
Given
$x=25+6t^2$ —(1)
$y=-50-20t+8t^2$ —(2)
Now at t=0
x=25 and y=-50
Differentiating equation 1 and 2 wrt
$ \frac {dx}{dt}=12t$ –(3)
$\frac {dy}{dt}=-20+16t$ –(4)
At t=0
$\frac {dx}{dt}=0$
$\frac {dy}{dt}=-20$
So magnitude of velocity =20 m/s
Differentiating equation 3 and 4 wrt
$ \frac {d^2x}{dt^2}=12$
$ \frac {d^2y}{dt^2}=16$
At t=0
$a_x=12$ and $a_y=16$
Direction of acceleration=$tan ^{-1} (\frac {16}{12})=tan^ {-1} (4/3)$
Magnitude=$20 \ m/s^2$

Question 3
Two particles X and Y travel along the x and y axis with respective velocities
$\mathbf{v_1} = 2\mathbf{i}$ m/sec
$\mathbf{v_2} = 3\mathbf{j}$ m/sec
At t=0 they are at
$x_1 = -3 \ m$ and $y_1=0$
$x_2= 0$ and $y_2=-3$ m
Find the vector which represents the position of Y relative to X as a function of t
$\mathbf{i}$ and $\mathbf{j}$ are respective unit vectors along x and y direction

Solution
Position of X after time t
$\mathbf{r_1}=(-3 + 2t)\mathbf{i}$
Position of Y after time t
$\mathbf{r_2}=(-3 + 3t)\mathbf{j}$
Relative vector of Y wrt to X
$= \mathbf{r_2} – \mathbf{r_1}$
Or =
$=3t -3) \mathbf{j} + (3-2t) \mathbf{i}$

Question 4
A light rod of length 2 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section area $0.1 \ cm^2$ and the other is made of brass of cross-section $0.1 \ cm^2$. Find out the position along the rod at which weight may be hung to produce
(a) equal stress in both wires
(b) equal strain in both wires

Young’s modulus of elasticity of brass and steel are $10 \times 10^{11} \ N m^{-2}$ and $20 \times 10^{11} \ Nm^{-2}$ respectively

Solution
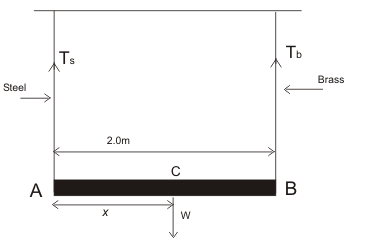
(a) AB is a rod of length L=200 cm=2 m. Suppose weight W is hung at C at a distance x from A as shown below in the figure. If $T_s$ and $T_b$ are the tensions in the steel and brass wires respectively then

stress in steel wire = $\frac {T_s}{A_s}$
stress in brass wire = $\frac {T_b}{A_b}$
Where $A_s$ and $A_b$ are the cross-sectional area of the steel and brass wire respectively.
Stress in each wire will be equal to
$\frac {T_s}{A_s} =\frac {T_b}{A_b}$
or
$ \frac {T_s}{T_b} = \frac {A_s}{A_b} = \frac {1}{ 2}$

Since the system is in equilibrium , the moments of force $T_s$ and $T_b$ about C will be equal, i.e.,
$T_s \times x = T_b \times ( 2.0 – x )$
or,
$ \frac {T_s}{T_b} = \frac {20 – x}{x}$
or
$\frac {1}{2} = \frac {20 – x}{x}$
which gives x = 4 3 = 1.33 m = 133.3 cm . Hence to produce equal stress in two wires , the weight should be hung at a distance 1.33.3 cm from the end A.
(b) $strain = \frac {stress}{Y} = \frac {T}{AY}$ . Strain in two wires will be equal if
$\frac {T_s}{A_sY_s} =\frac {T_b}{A_bY_b}$
or
$\frac {T_s}{T_b} = \frac {A_s Y_s}{A_b Y_b} = 1$
or, $T_s = T_b$ in this case. Equating the moments about C we have
$T_s \times x = T_b \times ( 2.0 – x )$ or, $x = 2.0 – x$
This gives x=1.0m=100 cm . Hence to produce equal strains in two wires, the weight should be hung at centre of the rod AB.

Question 5
A particle moves in a plane such that its velocity at t=0
$\mathbf{v_0}=2\mathbf{i} + 3\mathbf{j}$
The particle has constant acceleration
$\mathbf{a}= \mathbf{i} – 9\mathbf{j}$
Find the direction and magnitude of the velocity after t=1 sec

Solution
We know that velocity vector is given by the equation
$\mathbf{v} = \mathbf{u} + \mathbf{a}t$
Here $\mathbf{v_0}=2\mathbf{i} + 3\mathbf{j}$
$\mathbf{a}= \mathbf{i} – 9\mathbf{j}$
t=1
So,
$\mathbf{v} = 3\mathbf{i} + 4\mathbf{j}$
So magnitude=5
And direction= $tan^{-1} (4/3)$

Question 6
Two masses $m_1$ and $m_2$ are connected by a spring of force constant k and are placed on a smooth horizontal surface. Show that if the masses are displaced slightly in opposite directions and released, the system will execute the simple harmonic motion. Calculate the frequency of oscillation.

Solution

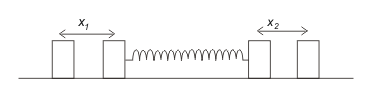
Let the masses $m_1$ and $m_2$ be displaced by amount $x_1$ and $x_2$ respectively from their equilibrium position in opposite directions so that the stretch in the spring will be $x=x_1+x_2$. Due to this stretch a restoring force kx will act on each mass and so equation of mass $m_1$ would be
$m1 \frac {d^2 x_1}{dt^2} = – kx$
$\frac {d^2 x_1}{dt^2}= -(\frac {k}{m_1}) x$

Similary for mass $m_1$ would be
$m2 \frac {d^2 x_2}{dt^2} = – kx$
$\frac {d^2 x_2}{dt^2}= -(\frac {k}{m_2}) x$

But as $x = x_1 + x_2$
we have
$\frac {d^2 x}{dt^2}=\frac {d^2 x_1}{dt^2} + \frac {d^2 x_2}{dt^2}$
Substituting from above
$\frac {d^2 x}{dt^2}= – k(\frac {1}{m_1} + \frac {1}{m_2}) x$
or
$\frac {d^2 x}{dt^2}= – (\frac {k}{m}) x$
Where $\frac {1}{m}=\frac {1}{m_1} + \frac {1}{m_2}$
or
$\frac {d^2 x}{dt^2}= – \omega ^2 x$
Where $\omega ^2= \frac {k}{m}$
which is the standard equation of SHM of a particle of mass m connected to a spring of force constant k. Frequency of oscillations is
$f = \frac {1}{2 \pi} \sqrt {\frac {k}{m}} =\frac {1}{2 \pi} \sqrt {\frac {km_1m_2}{m_1+ m_2}}$

Question 7
Two projectiles are thrown with different velocities and at different angles so as to cover the same maximum height. Show that the sum of times taken by each to reach the highest point is equal to the total time taken by either of the projectiles.

Solution
If the two projectiles are thrown with velocities $u_1$ and $u_2$ at angles $\theta _1$ and $\theta _2$ with horizontal , then their maximum height will be,
$H_1 = \frac {u_1^2 sin^2 \theta _1}{2g}$ and $H_2 = \frac {u_2^2 sin^2 \theta _2}{2g}$
but $H_1 = H_2$
Therefore,
$\frac {u_1^2 sin^2 \theta _1}{2g} = \frac {u_2^2 sin^2 \theta _2}{2g}$
or, $u_1 sin \theta _1 = u_2 sin \theta _2$ —(1)

Times of flight for the two projectiles are

$T_1 = \frac {2u_1 sin \theta _1}{g}$ and $T_2 = \frac {2u_2 sin \theta _2}{g}$
Making use of equation 1 we get
$T_1 = T_2 = \frac {2u_1 sin \theta _1}{g} = \frac {2u_2 sin \theta _2}{g}$
Times taken to reach the heighest point in the two cases will be ,
$t_1 = \frac {2u_1 sin \theta _1}{g}$ and $t_2 = \frac {u_2 sin \theta _2}{g}$
$t_1 + t_2 = \frac {2u_1 sin \theta _1}{g} + \frac {u_2 sin \theta _2}{g} =\frac {2u_1 sin \theta _1}{g} = \frac {2u_2 sin \theta _2}{g}$ (by using equation 1)
So, $t_1 + t_2$ =time of flight of either projectile

Question 8
Two satellites $S_1$ and $S_2$ revolve around a planet in co-planar circular orbits in the same sense. Their periods of revolution are 1 hour and 8 hours respectively. The radius of the orbit of Satellite $S_1$= $10^4 \ Km$. When $S_2$ is closest to $S_1$,find
(a) Speed of $S_2$ relative to $S_1$ and
(b) the angular speed of $S_2$ actually observed by an astronaut in $S_1$.

Solution
The period T of revolution of a satellite revolving round a planet of mass min circular orbit of radius r is given by
$T^2 = \frac {4 \pi^2 r^3}{GM}$
For satellite S1 : $T_1^2 = \frac {4 \pi^2 r_1^3}{GM}$
For satellite S2 : $T_2^2 = \frac {4 \pi^2 r_2^3}{GM}$
Hence
$\frac {T_2^2}{T_1^2} = \frac {r_2^3}{r_1^3}$
This is Kepler’s law of periods. Thus
$r_2^3 = r_1^3 (\frac {T_2^2}{T_1^2})$
Given that $r_1 = 10^4 \ Km = 10^6 \ m$, $T_1 = 1$ hour and $T_2 = 8$ hr. Therefore,
$r_2^3 = ( 10^6)^3 ( 8/ 1 )^2 = 64 \times 10^{18}$
or,
$r_2 = 4 \times 10^6 \ m = 4 \times 10^4 \ Km$
(a) The orbital speeds of satellite $S_1$ and $S_2$ respectively are
$v_1 = \frac {2 \pi r_1}{T_1} = 2 \pi \times 10^4$ Km / hr
$v_2 = \frac {2 \pi r_2}{T_2} = \pi \times 10^4$ Km / hr
The magnitude of speed of $S_2$ relative to $S_1$ is
$| v_2 – v_1 | =\pi \times 10^4 \ Km/hr = 3.14 \times 10^4 \ Km/hr$

(b) The angular speed of $S_2$ relative to $S_1$ is
$\omega = \frac {v_2 – v_1}{ r_2 – r_1} = – \frac {3.14 \times 10^4 }{4 \times 10^4 – 10^4} = – \frac {3.14}{3} = – 2.19 \times 10^4$ rad/s

The negative sign indicates the sense of rotation of ? is opposite to sense of revolution of satellites.

Question 9
Two bodies of masses $M_1$ and $M_2$ are placed at a distance d apart. What is the potential at the position where the gravitational field due to them is zero?
(a) $-\frac {G(\sqrt {M_1} + \sqrt {M_2})}{d}$
(b) $- \frac {G(M_1 + M_2 + 2 \sqrt {M_1 M_2})}{d}$
(c) $\frac {G(M_1 – M_2)}{d}$
(d) None of these

Solution
Let the gravitational field be zero at a point distant x from $M_1$
$ \frac {GM_1}{x^2} = \frac {GM_2}{(d – x)^2}$
$\frac {x}{d – x} = \frac {\sqrt {M_1}}{\sqrt {M_2}}$
$x \sqrt {M_2} = \sqrt {M_1} d – x \sqrt {M_1}$
$x [ \sqrt {M_1} + \sqrt {M_2} ] = \sqrt {M_1} d$
$x = \frac {d \sqrt {M_1}}{\sqrt {M_1} + \sqrt {M_2}}$
$d – x = \frac {d \sqrt {M_2}}{\sqrt {M_1} + \sqrt {M_2}}$

Potential at this point due to both the masses will be
$= – \frac {GM_1}{x} – \frac {GM_2}{d – x}$
Subsituting the values of x and d-x
$= – \frac {G( M_1 + M_2 + 2 \sqrt {M_1 M_2})}{d}$

Question 10
A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it
Density of wood=$800 \ kg/m^3$
Spring constant=50 N/m
$g=10 \ m/s^2$
(a) 1 N
(b) .3 N
(c).32 N
(d) .5 N

Solution
The specific gravity of the block =.8 ,hence the height inside water =$3 \ cm \times .8=2.4 \ cm$.
The height outside water =3 cm – 2.4cm=.6 cm

Suppose the maximum weight that can be put without wetting it is W. The block, in this case, is completely immersed in the water

The volume of the displaced water =volume of the block= $27 \times 10^{-6} \ m^3$
Hence the force of buoyancy
$=(2.7 \times 10^{-6}) \times (1000) \times (10)=.27$ N
Now the spring is compressed by .6 cm and hence the upward force exerted by the spring
$=50 \times 0.6 \times 10^{-2}=0.3 \ N$
Now
The force of buoyancy and spring force taken together balance the weight of the block plus the weight W put on the block
i.e
.27+.3=w+W
Now weight of the block =$(27 \times 10^{-6}) \times (800) \times (10)=.22 \ N$
So W=.35N

Question 11
The cylindrical tube of a spray pump has a radius R and one end of which has m fine holes each of radius r. If the speed of the flow of liquid is V, the speed of ejection of the liquid through the holes is
(a) $\frac {VR^2}{r^2}$
(b) $\frac {V r^2}{R^2 m}$
(c) $\frac {VR^2}{mr^2}$
d) $ \frac {VR}{rm}$$

Solution
From continuity equation
$A_1v_1=A_2v_2$
$ \pi R^2V=m \pi r^2 v$
or
$v = \frac {V R^2}{r^2 m}$

Question 12
A body is subjected to a constant force F in newton given by
$\mathbf{F}=-\mathbf{i}+2\mathbf{j}+3\mathbf{k}$
Where $\mathbf{i}$,$\mathbf{j}$ and $\mathbf{k}$ are the unit vectors across x,y,z co-ordinates system
(i) what is the work done by this force in moving a distance 4 m along the z-axis?
(a) 12J
(b) 8 J
(c) 11.2 J
(d) None of these
(ii) what is the work done by this force in moving a distance 3 m along the y-axis?
(a)2 J
(b)4 J
(c)6 J
(d) 8 J
(iii) what is the total work done by the force in moving the body through a distance of 4m along the z-axis and then 3 m along the y axis?
(a)20 J
(b) 18 J
(c) 10 J
(d) None of these
(iv) Which of these are scalar quantity
(a) work done
(b) force
(c) displacement
(d) distance

Solution
The force in newton is given by
$\mathbf{F}=-\mathbf{i}+2\mathbf{j}+3\mathbf{k}$
(i) Displacement along z-axis
$\mathbf{d}=4\mathbf{k}$
Therefore workdone is
$W_1=\mathbf{F}.\mathbf{d}=(-\mathbf{i}+2\mathbf{j}+3\mathbf{k}).(4\mathbf{k})=-4\mathbf{i}.\mathbf{k}+8\mathbf{j}.\mathbf{k}+12\mathbf{k}.\mathbf{k}$
Now $\mathbf{i}.\mathbf{k}=0$ and $\mathbf{j}.\mathbf{k}=0$ as $\mathbf{i}$ and $\mathbf{j}$ are perpendicular to $\mathbf{k}$ and $\mathbf{k}.\mathbf{k}=1$
Hence $W_1=12 \ J$
(ii) Similary Displacement along y-axis is
$\mathbf{d}=3\mathbf{j}$
Hence workdone in this case is
$W_2=\mathbf{F}.\mathbf{d}=(-\mathbf{i}+2\mathbf{j}+3\mathbf{k}).(3\mathbf{j})=6 \ J$
(iii) Since workdone is scalar ,the total workdone is just the algebric sum of $W_1$ and $W_2$
W=12+6=18J
(iv) Workdone and distance are scalar quantity

Question 13
A moving particle A of mass m of velocity u makes a head-on collision with a particle B of mass 2m which is initially at rest
(i) Find the velocity of particle A and velocity of particle B after the collision
(a) -u/5,4u/5
(b) -u/2,u/2
(c) -u/3,2u/3
(d) None of these
(ii) which of the following is true
(a) Linear momentum remain conserved
(b) Energy is also conserved
(c) Velocity of Center of mass of the system remain constant
(d) None of these
(iii) Find the fractional loss of the energy of particle A due to collision
(a) 8/9
(b) 1/9
(c) 2/3
(d) 4/5

Solution
Let $v_1$ and $v_2$ be the velocities of the particles after collision
From the principle of the law of conservation of Linear momentum,we have
$mu=mv_1+2mv_2$
or
$u-v_1=2v_2$ —(1)
From the principle of the law of conservation of energy
$\frac {1}{2} m u^2 =\frac {1}{2} mv_1^2 + \frac {1}{2} 2mv_2^2$
or
$u^2-v_1^2=2v_2^2$
$(u-v_1)(u+v_1)=2v_2^2$ —(2)
From equation (1) and (2),we have
$2v_2(u+v_1)=2v_2^2$
or
$u+v_1=v_2$
or
$2(u+v_1)=2v_2$ —–(3)

From equation (1) and (3)
$v_1=- u/3$

Substituting this value we get

$v_2=2u/3$

Velocity of center of mass will remain constant as no external forceacting

Now Initial Kinetic energy

$K_i = \frac {1}{2}m u^2$
$K_f = \frac {1}{2} m v_1^2$
Loss in kinetic energy
$ \Delta K=K_i-K_f$
Fractional loss
$f = \frac {\Delta K}{K_i} = \frac {u^2 – v_1^2}{u^2} = 1 – (\frac {v_2}{u})^2 = 1 – (\frac {1}{3})^2 = \frac {8}{9}$

Question 14
A planet of mass M and radius R has a satellite of mass m revolving in a circular orbit around it at a height h above the surface of the planet.
During its motion, the satellite begins to experience a resistive force (due to cosmic dust) $F=kv$ where k is constant and v is the instantaneous velocity of the satellite
(i) Find the initial velocity of the planet?
(a) $v_0 = \sqrt {\frac {Gm}{R + h}}$
(b) $v_0 = \sqrt {\frac {GM}{R + h}}$
(c) $v_0 = \sqrt {\frac {GMh}{ R}}$
(d) None of these
(ii) Find the total initial energy of the satellite?
(a) $E = – \frac {GMm}{2R}$
(b)$E = – \frac {GMm}{ 2 ( R + h )}$
(c)$E = – \frac {GMm}{ 2 ( R ? h )}$
(d)$E = – \frac {GMm}{ 2 ( R + 2 h )}$
(iii)Find the velocity of the planet when it touches the surface of the earth?
(a) $v_f = \sqrt {\frac {GM}{R ? h}}$
(b) $v_f = \sqrt {\frac {Gm}{ R}}$
(c) $v_f = \sqrt {\frac {G ( M + m )}{ R}}$
(d) $v_f = \sqrt {\frac {GM}{ R}}$
(iv) Find the time taken by the satellite to fall from its orbit to the surface of the planet?
(a) $t = \frac {m}{2k} log_e \frac {h}{R}$
(b) $t = \frac {m}{2k} log_e ( 1 + \frac {2h}{R})$
(c)$t = \frac {m}{2k} log_e ( 1 – \frac {h}{R})$
(d) $t = \frac {m}{2k} log_e ( 1 + \frac {h}{R})$

Solution
Orbital radius =R+h
The orbital speed v of the satellite is given by
$ \frac {mv_0^2}{ R + h} = \frac {GMm}{ ( R + h )^2}$
or
$v_0 = \sqrt {\frac {GM}{R + h}}$

Now total energy in the orbit is given by

E=PE+KE
$E = – \frac {GMm}{r} + \frac {1}{2} m v^2$
Now substituting the initial velocity in this
$E = 0 \frac {GMm}{2( R + h )}$

Final Orbital radius =R
$v_f = \sqrt {\frac {GM}{ R}}$

Let t be the time taken by the satellite to fall from its orbit to the surface of the planet i.e t is the time taken for the speed to change from v0 to vf .if v is the instantanous speed of the satellite,the resistive force acting on it at that instant is given to be

$F=kv$
or$m \frac {dv}{dt} = k v$
or
$\frac {1}{v} dv = \frac {k}{m} dt$

Integrating we have?

$\int_{v_i}^{v_f} \frac {1}{v} dv = \int_{0}^{t} \frac {k}{m} dt$

$log_e \frac {v_f}{ v_i} = \frac {k}{m} t$
Substituting the values of $v_f$ and $v_i$ ,we get
$t = \frac {m}{k} log_e \sqrt {\frac {R+h}{R}}$
$t = \frac {m}{2k} log_e ( 1 + \frac {h}{R})$

Question 15
A copper calorimeter of water equivalent 60 g contains 600g of water at 300 °C. The calorimeter and contents are given a supply of heat at the rate of 100 cal/s. No heat is lost to the surrounding from the calorimeter.
Specific heat of capacity of water =1 cal/g °C
Latent heat of steam =540 cal/g
(i) Find the heat required to raise the temperature of water from 300C to boiling point
(a)46200 cal
(b) 42000 cal
(c) 42010 cal
(d) none of these
(ii) Find the time taken to bring the water to its boiling point
(a) 6 min 42 s
(b) 7 min 42 s
(c) 7 min
(d) 8 min
(iii)Time required to boil away the 100 g of water
(a) 17 min
(b) 11 min
(c) 12 min 12 sec
(d) 16 min 42 sec

Solution
The water equivalent of calorimeter =60 g
calorimeter + water contained in it are together equivalent to 60+600=660 g of water
Now
Heat required to raise the temperature of water from 30 to 100 is given by

$Q=mc \Delta T=660 \times 1 \times 70 =46200$ cal

Now the heat is supplied at the rate of 100 cal/sec, So the time required to get this amount to boiling point

$t=\frac {46200}{100} $=7 min 42s

Now to boil away 100 g of water at its boiling point, the quantity of heat required is

$Q=mL=100 \times 540=54000$ cal

Now again time required

t=54000/100=540sec=9 min

So total time required=7 min 42sec +9 min=16 min 42 sec

Question 16
The walls of a closed cubical box of edge 50 cm are made of material of thickness 1 mm and thermal conductivity $4 \times 10^{-4} \ cal s^{-1} cm^{-1}C^{-1}$.
The inside temperature of the box is at 130 °C and outside at 30 °C. The temperature inside the interior of the box is maintained with the help of a heater.
The heater is connected to 400 V DC voltage and has resistance R.
(i) which of the following formula would be use to find heat loss/sec through walls of the cubical box
(a) $\frac {KA ( T_2 – T_1 )}{ d}$
(b) $\frac {K ( T_2 – T_1 )}{Ad}$
(c) $\frac {Kd}{ A ( T_2 – T_1 )}$
(d) None of these
(ii) Find the value of R
(a)R=5.35 ohm
(b)R=5 ohm
(c) R=6 ohm
(d) R=6.35 ohm

Solution
The heat transmitted per second through the walls of the closed box is given by
$\frac {Q}{t} =\frac {KA ( T_2 – T_1 )}{ d}$
Where A is the total area of the box as heat would be lost across all the sides
Now we have

$K=4 \times 10^{-4} \ cal s^{-1} cm^{-1}C^{-1}$.
$A=6 \times 50 \times 50 \ cm^2$
d=.1 cm
$T_2-T_1=100$
Substituting all the values in the above equation
$Q/t= 6000$ cal/s
The heat lost through the wall should be compensated through the heater to maintain the same temperature difference
Now heat produced by the Heater
$H =\frac {V^2}{ R} \ Joule = \frac {V^2}{4.2 R} \ cal$
Now Heat Generated through Heater = Heat lost through the heat transfer across the box
$\frac {V^2}{4.2 R} = 6000$
We have V=400 V
or R=6.35 ohm

Question 17
A ring of radius 0.1 m is made out of a thin metallic wire of area of cross-section $10^{-6} \ m^2$. The ring has a uniform charge of $\pi$ Coulomb. Find in change the radius of the ring when a charge of $10^{-8}$ C is placed at the center of the ring. Young’s modulus of the metal is $2 \times 10^{11} \ Nm^{-2}$.

Solution
Given that radius of the ring is r=0.1 m . Therefore charge per unit length of the ring is
$\lambda = \frac {Q}{2 \pi r} = \frac {\pi}{2 \pi (.1)} = 5 \ C/m$

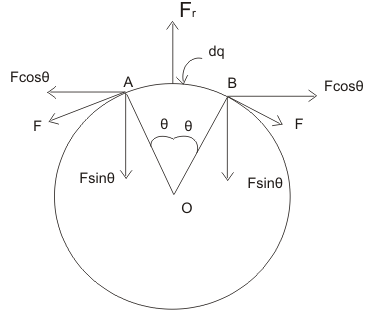
Consider very small element AB of the wire as shown below in the figure. Let dl=AB be the length of the element.

Then the charge on the element is
$dq= \lambda dl$
The charge q0 at the center repels the element with the repulsive force
$F_r=\frac {1}{4 \pi \epsilon _0} \times \frac {q_0 dq}{r^2}$
As a result, tension is developed in the wire. This force acts tangentially at the ends A and B of the element. As is clear from the figure horizontal components $Fcos \theta$ cancels each other. The vertical components $Fsin \theta$ are directed downwards. Here $2 \theta$ is the angle which the element AB makes with the center of the ring. As dl?o the two components become collinear and add up to 2Fsin? which balances with the upward component Fr at equilibrium. Thus
$2Fsin \theta=F_r$
As dl is very small, $\theta$ is also small and for small values of $\theta$ , $sin \theta = \theta$ , where $\theta$ is in radians. Hence
$2F \theta =F_r$
But
$2 \theta = \frac {dl}{r}$
or
$\theta = \frac {dl}{2r}$
Therefore
$\frac {F dl}{r} = F_r$
or
$\frac {F dq}{\lambda r} = F_r$
$\frac {F dq}{\lambda r}=\frac {1}{4 \pi \epsilon _0} \times \frac {q_0 dq}{r^2}$
$F= \frac {1}{4 \pi \epsilon _0} \frac {\lambda q_0}{r}$
Substituting the values
$F=4500 N$
Now
Strain = $\frac { \Delta r}{r}$
Also
$Y = \frac {stress}{strain}$
$ \Delta r = \frac {r F_r}{A Y}$
Substituting the values
$=2.25 \ mm$

Question 18
A parallel plate capacitor contains one mica sheet of thickness $A_1=1.0 \ mm$ and one fiber sheet of thickness $B_1=.5 \ mm$. The dielectric constants of mica and fibre are 8 and 2.5 respectively. Fiber breaks down in an electric field of $6.4 \times 10^6 Vm^{-1}$. What maximum voltage can be applied to the capacitor?

Solution
Let $\sigma$ be the surface charge density on each plate of the capacitor .Let $E_1$ and $E_2$ be the electric fields in the mica($K_1$) of thickness $A_1=1.0 \ mm$ and fibre($K_2$) of thickness $B_1=.5 \ mm$.Then
$E_1=\frac {\sigma} {K_1 \epsilon _0}$
and
$E_2=\frac {\sigma }{K_2 \epsilon _0}$

or $E_1=(\frac {K_2}{K_1})E_2$ —-(1)

The maximum possible value of E2(dielectric strength of the fibre) is $6.4 \times 10^6 Vm^{-1}$
Therefore maximum $E_1$ can be equation (1)
$E_1=(2.5/8)6.4 \times 10^6=2.0 \times 10^6 \ Vm^{-1}$.
So maximum voltage that can be applied
$V=E_1A_1+E_2B_1$
Substituting values from above
$V=5200 \ V$

Question 19
Two isolated metallic spheres of radii R and 2R are charged such that both these have the same charge density $\sigma$. The spheres are located far away from each other and connected by a thin conducting wire. Find the new charge density on the bigger sphere

Solution
Initial charges on sphere of radius R and 2R respectively are
$Q_1= \text{surface area} \times \text{charge density} = 4 \pi R^2 \sigma$
and
$Q_2=4 \pi (2R)^2 \sigma = 16 \pi R^2\sigma$
therefore
$Q_1+Q_2=4 \pi R^2 \sigma +16 \pi R^2\sigma$ —(1)
As the charges are different, their initial potentials are also different. When the spheres are connected by long thin conducting wire, the charges are redistributed untill their potentials become equal. Let $Q’_1$ and $Q’_2$ be the new charges on spheres of radii R and 2R respectively, their common potential is
$V = \frac {1}{4 \pi \epsilon _0} \frac {Q’_1}{R} = \frac {1}{4 \pi \epsilon _0} \frac {Q’_2}{2R}$
which gives
$Q’_1 = \frac {Q’_2}{2}$
Therefore,
$Q’_1 + Q’_2 = 3Q’_2/ 2$
From Law of conservation of charge
$Q_1+Q_2=Q’_1+Q’_2$
Using equation 1 and 2 we have
$Q’_2 = \frac {40 \pi R^2 \sigma}{3}$
The new charge density on the bigger sphere of radius R is
$\sigma ‘ = \frac {Q’_2}{ 4 \pi ( 2 R )^2} = \frac {5 \sigma}{6}$

Question 20
An uncharged conductor has a cavity inside it. Somewhere in the cavity is a charge +q. What can you say about the electric field
(a) inside the cavity
(b) within the conductor
(c) outside the conductor

Solution

(a) The cavity is electrically isolated from the conductor surrounding it. Since it has a charge, the electric field inside the cavity non zero.
(b) The charge +q induces an opposite charge -q on the wall of the cavity which distributes itself in such a way that its field cancels that of +q for all points in the conductor. Hence there is no net electric field within the conductor as shown in the figure.

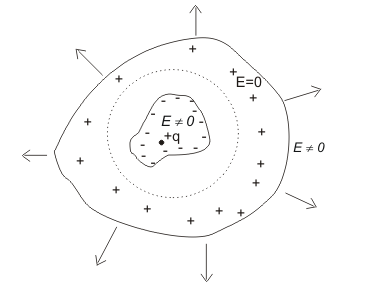
(c) Since the conductor carries no net charge, this leaves charge +q to distribute over the surface of the conductor. For all points outside the conductor, the only field that survives is the field of the leftover charge +q on the outer surface. This charge produces a non-zero field in the region surrounding the conductor. To show that charge -q is induced on the inner surface of the cavity, surround the cavity with a Gaussian surface as shown in the figure. Since every point on this surface is inside the conductor, the surface integral of E over this surface vanishes, and hence by Gauss’s Law, the charge enclosed by this surface is zero i.e., $q_{enc} = q + q_{ind}$, where $q _{ind}$ is the charge induced on the inner surface which is equal to -q.

Question 21
The magnitude of electric field E in the annular region of a charged cylindrical capacitor
(a) is the same throughout
(b) is higher near the outer cylinder than near the inner cylinder
(c) varies as $\frac {1}{r}$ where r is the distance from the axis
(d) varies as $\frac {1}{r^2}$ where r is the distance from the axis

Solution
The magnitude of the electric field in the annular region of a charged cylindrical capacitor is given by
$E = \frac {1}{4 \pi \epsilon _0} \frac {2 \lambda}{ r}$
where $\lambda$ is charge per unit length and r is the distance from the axis of the cylinder. Hence $E \alpha \frac {1}{r}$
Answer is (c)

Question 22
A parallel combination of 0.1 M ? resistor and 10 ?F capacitor is connected across 1.5V source of negligible resistance. The time (in seconds) required for the capacitor to get charged upto 0.75V is approximately
(a) infinite
(b) $log_e 2$
(c) $log_{10} 2$
(d) zero

Solution
There is no resistance in the part of the circuit containing a battery and the capacitor, i.e., R=0 in this circuit. Hence the time constant which is equal to RC would be equal to zero.
Answer: (d)

Question 23
An electron of mass m and charge -q is at rest at origin on the x-axis. It is subjected to an electric field which is given below
$\mathbf{E}=E_0 sin \omega t \mathbf{i}$
(i) Find out the position of the electron as a function of time
(a)$x = – \frac {qE_0 \omega ^2}{m} t + \frac {qE_0 \omega ^2}{m} cos \omega t $
(b) x = $x = – \frac {qE_0 \omega ^2}{m} t – \frac {qE_0 \omega ^2}{m} cos \omega t $
(c) $x = – \frac {qE_0 \omega ^2}{m} t + \frac {qE_0 \omega ^2}{m} sin \omega t $
(d) $x = – \frac {qE_0 \omega ^2}{m} t – \frac {qE_0 \omega ^2}{m} sin \omega t $
(ii) Find out the velocity of the electron as a function of time
(a)$v = \frac {qE_0 \omega}{m} ( cos \omega t – 1 )$
(b)$v = \frac {qE_0 \omega}{m} ( cos \omega t + 1 )$
(c)$v = \frac {qE_0 \omega}{m} ( sin \omega t – 1 )$
(d)$v = \frac {qE_0 \omega}{m} ( sin \omega t – 1 )$

Solution
The force on electron due to electric field
$\mathbf{F}=-q\mathbf{E}$
$\mathbf{F}=-qE_0 sin \omega t \mathbf{i}$
Acceleration
$\mathbf{a}= – \frac {qE_0}{m} sin \omega t \mathbf{i}$
or
$\frac {dv}{dt} = -\frac {qE_0}{m} sin \omega t$
Integrating we get
$v = \frac {qE_0 \omega}{m} ( cos \omega t – 1 ) + a$
Where a is integration constants
Since v=0 at t=0
$v = \frac {qE_0 \omega}{m} ( cos \omega t – 1 )$

Now again

$\frac {dx}{ dt} = \frac {qE_0 \omega}{m} ( cos \omega t – 1 )$
Integrating we get
$x = – \frac {qE_0 \omega ^2}{m} t – \frac {qE_0 \omega ^2}{m} sin \omega t + b$
Where b is integration constants
Now x=0 at t=0
So
$x = – \frac {qE_0 \omega ^2}{m} t – \frac {qE_0 \omega ^2}{m} sin \omega t $

Question 24
Find the capacitance of the three parallel plates each of area A $meter^2$ and separated by $d_1$ and $d_2$ meter. The in-between spaces are filled with dielectrics of relative permittivity $\epsilon _1$ and $\epsilon _2$. The permittivity of the free space is $\epsilon _0$

Solution
The system is equivalent to two parallel plate capacitors connected in series. The spaces between the plates of the capacitors are filled with dielectrics media whose dielectrics constants K are $\epsilon _1$ and $\epsilon _2$. The dielectrics constant are also called relative permittivity.

Therefore the capacitances of two capacitors are
$C_1 = \frac {\epsilon _1 \epsilon _0 A}{d_1}$
$C_2 = \frac {\epsilon _2 \epsilon _0 A}{d_1}$

If C is the equivalent capacitance of the system,then
$\frac {1 }{C} = \frac {1}{C_1} + \frac {1}{C_2}$
or
$C = \frac {\epsilon _0 \epsilon _1 \epsilon _2 A }{\epsilon _2 d_1 + \epsilon _1 d_2}$

Question 25
A circuit consists of a series combination of a 50mH inductor and a $20 \mu F$ capacitor. The circuit is connected to an AC supply of 220V and 50hz.
The circuit has the value of R=0
(i) Which of the following is correct for the circuit?
(a) $I_0=2.17$ A ,$I_{rms}= 1.53$ A
(b) $I_0=5.1$ A ,$I_{rms}= 3.6$ A
(c) $V_0=311$ V ,$V_{rms}=200$ V
(d) None of these

(ii) which of the following is false
(a) Voltage drop across the inductor is 23.1 V
(b) Voltage drop across the capacitor is 243 V
(c) Voltage drop across the inductor is 243 V
(d) Voltage drop across the capacitor is 23.1 V

(iii) which of the following is true

(a) Average power transferred to the inductor is zero
(b) Average power transferred to the capacitor is zero
(c) Average power absorbed by the circuit is zero
(d) None of the above

Solution
The following quantities are given in the question

$L=50 \ mH=50 \times 10^{-3} \ H$
$C=20 \mu F=20 \times 10^{-6} F$
$V_{rms}=220 V$
f=50hz or $\omega =2 \pi f=100 \pi $ rad/sec
Now
$V_0 = \sqrt {2} V_{rms} = 311$ V
The peak current is given by the below equation in LC circuit
$I_0 = \frac {V_0}{Z}$
Where
$Z = \omega L – \frac {1}{\omega C}$
Substituting the values from above
$I_0=-2.17$ A
So magnitude is
$I_0=2.17$ A
$I_{rms}=\frac {I_0}{\sqrt 2} =1.53$ A
Voltage drop across inductor is given by
$V_L=I_{rms} \omega L=23.1$ V

Voltage drop across capacitor is given by
$V_C= \frac {I_{rms}}{\omega C} =243$ V
Since in both inductor and capacitor, voltage and current are at a right angle, no power will be transferred to them
Hence total power absorbed is also zero

Question 26
In the chemical analysis of a rock, the mass ratio of the two radioactive isotopes A and B is found to be 100:1. The mean lives of the two isotopes are $4 \times 10^9$ years and $2 \times 10^9$ years respectively. If it is assumed that, at the time of formation of the rock, the atoms of the two isotopes were in equal proportion.
Given the ratio of the atomic weight of the two isotopes is 1.02:1
Find the age of the rock
(a)$1.83 \times 10^9$ years
(b)$1.9 \times 10^{10}$ years
(c)$1.7 \times 10^{10}$ years
(d)$1.83 \times 10^{10}$ years

Solution

Given
$M_A:M_B= 1.02:1$
$N_1(0):N_2(0)=1:1$

Let $N_1$ be the no of moles of isotope A in the rock

Let $N_2$ be the no of moles of isotope B in the rock

Let $m_A(t)$ and $m_B(t)$ be the masses of the two isotopes respectively

Now it is given

$m_A(t): m_B(t) =100:1$

or
$\frac {m_A}{m_B} = \frac {N_1}{N_2} \times {M_A}{M_B}$

As we know

$m_A(t): m_B(t) =100:1$
$M_A:M_B= 1.02:1$
So

$N_1:N_2=100:1.02$

Now from the equation of radioactivity for two isotopes

$N_1(t) = N_1(0) e^{-t/ \tau _1}$
$N_2(t) = N_2(0) e^{-t/ \tau _2}$

Dividing these two equation and substituting the values from above
$\frac {100}{1.02} = e^{-t ( \frac {1}{\tau _1} – \frac {1}{\tau _2})}$
or
$-t(\frac {1}{\tau _1} – \frac {1}{\tau _2}) ) = log_e \frac {100}{1.02}$

Putting values for mean lives,we get
$t=1.83 \times 10^{10}$ years

Hope you like this JEE advanced physics questions

Also Reads
sin cos tan table
physics notes for iit jee
https://jeeadv.ac.in/