What is Many one Function
A many-to-one function is a function in which multiple elements in the domain may map to the same element in the range. In other words, a single element in the range can have more than one preimage in the domain.
Definition
A function f : A -> B is said to be many one function if two or more elements of the set A has the same image in B
i.e there exists $x, y \in A$ such that $x \ne y$ and f(x) = f(y)
If a function is not one-one , it will be many one function
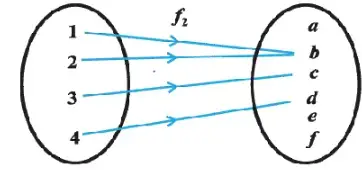
Examples
The Greatest integer function
f(x) = [x], rounds a real number x down to the nearest integer.
For example, f(3.8)=[3.8] = 3, f(-2.4)=[-2.4] = -3, and $f(\pi)=[\pi] = 3$
Since multiple real numbers can round down to the same integer, the floor function is many-to-one.
The absolute value function:
f(x) = |x|, returns the distance between x and 0 on the number line.
For example, f(3) =|3| = 3, f(2)=|-2| = 2, and |0| = 0.
Since both x and -x have the same absolute value, the absolute value function is many-to-one.
Square function
$f(x) =x^2$
for example $f(1) =1^2=1$ , $f(-1)= (-1)^2 = 1$
Since both x and -x have the same value, the square function is many-to-one.
Frequently Asked Questions:
Question 1
Can a function be both one-to-one and many-to-one?
Answer
No, a function cannot be both one-to-one and many-to-one. A one-to-one function maps each element in the domain to a unique element in the range, while a many-to-one function maps multiple elements in the domain to the same element in the range.
Question 2
Can a many-to-one function have an inverse function?
Answer
No, a many-to-one function does not have an inverse function. An inverse function is a function that maps each element in the range back to a unique element in the domain. Since a many-to-one function maps multiple elements in the domain to the same element in the range, its inverse function cannot map each element in the range back to a unique element in the domain.
Question 3
Is it possible for a function to be neither one-to-one nor many-to-one?
Answer
No, every function must be either one-to-one or many-to-one. If a function maps each element in the domain to a unique element in the range, it is one-to-one. If it maps multiple elements in the domain to the same element in the range, it is many-to-one.
Related Articles
