What is Wheat Stone Bridge?
A Wheatstone bridge is an electrical circuit used to measure an unknown electrical resistance by balancing two legs of a bridge circuit, one leg of which includes the unknown component. it was invented by Samuel Hunter Christie in 1833 and improved and popularized by Sir Charles Wheatstone in 1843.Although today digital multimeters provide the simplest way to measure a resistance, The Wheatstone Bridge can still be used to measure very low values of resistances down in the milli-Ohms range.
Principal For Wheat Stone Bridge
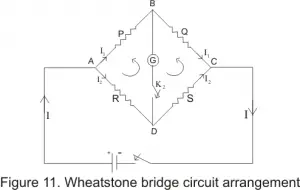
The general arrangement of Wheatstone bridge circuit is shown in the figure below. It is a four arms bridge circuit where arm AB, BC, CD and AD are consisting of electrical resistances P, Q, S and R respectively. Among these resistances P and Q are known fixed electrical resistances and these two arms are referred as ratio arms. An Galvanometer is connected between the terminals B and D through a switch K2. The voltage source of this Wheatstone bridge is connected to the terminals A and C via a switch K1 as shown. A variable resistor S is connected between point C and D. The potential at point D can be varied by adjusting the value of variable resistor. If we vary the electrical resistance value of arm CD the value of current I2 will also be varied as the voltage across A and C is fixed. If we continue to adjust the variable resistance one situation may comes when voltage drop across the resistor S that is I2.S is becomes exactly equal to voltage drop across resistor Q that is I1.Q. Thus the potential at point B becomes equal to the potential at point D hence potential difference between these two points is zero hence current through galvanometer is nil. Then the deflection in the galvanometer is nil when the switch K2 is closed.
Applying Kirchoff’Law we can easily find that in that condition
P/Q=R/S
Meter Bridge Experiment using Wheatstone Bridge Principle
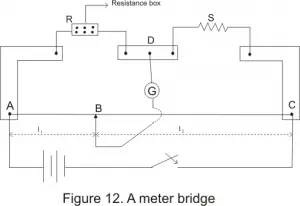
Meter bridge is based on the principle of wheat stone bridge and it is used to find the resistance of an unknown conductor or to compare two unknown resistance. The practical diagram is shown in the below figure
Calculation
R is Known Resistance
S is Unknown Resistance
P is Resistance across AB
Q is the Resistance between BD
AC is a 1m long wire made of maganin or constanan having uniform area of cross-section So that L1+L2=100
Assuming L1=L => L2=100-L
The unknown resistance ‘X’ of the given wire is obtained by relation :
X = RL2/L1= R(100-L)/L
And specific resistance of the material of a given a wire is obtained by =(3.14) r2X/l
where r = radius of the wire and l = length of wire.
Task of the Experiment
To find out the Unknown Resistance and radius of the wire using meterbridge. We need to take 5 reading and average out that for the calculation
Instruments required for the experiment
1) Meter bridge
2) Galvanometer
3) Resistance box
4) Unknown Resistance of length 1 m
5) connecting Wires
6) Screw gauge
7) One way key
8) Jockey
PROCEDURE :
Step 1) Collect all the instruments and make the connection as shown in figure above
Step 2) Take out some suitable resistance ‘R’ form the resistance box (R. B.).
Step 3) Touch the jockey at point A; see that there is a deflection in the galvanometer on one side, then touch the jockey on the point C of the wire, the deflection in the galvanometer should be on the other side. If it is so, your connections are correct.’
Step 4) Now find the position of null point where deflection in galvanometer becomes zero.
Note length AB (l) BC will be (100 – l).
Step 5) Repeat the above procedure for different values of ‘R’. Take atleast 5 readings
Step 6)Note the point where the galvanometer shows 0 deflections, this is called the balance point.
Step 7) Measure the length of the given wire using ordinary scale and the radius of the wire using screw gauge( Take five readings)
Table Of Observation
Table for Unknown Resistance (X)
| S.no | Values Of Known Resistance (R) | Balancing Length(L) | Value of Unknown Resistance (X=R(100-L)/L) |
| 1 | – | – | – |
| 2 | – | – | – |
| 3 | – | – | – |
| 4 | – | – | – |
| 5 | – | – | – |
Calculate the Mean Resistance of the Unknown Resistance= (Total Sum of the resistance of Unknown resistance from above 5 reading)/5
Table for Diameter (d)
LC of Screw Gauge=
Zero Correction=
| S.no | PSR | HSR | Corrected HSR=PSR+HSR.LC |
| 1 | – | – | – |
| 2 | – | – | – |
| 3 | – | – | – |
| 4 | – | – | – |
| 5 | – | – | – |
Mean diameter of the wire(d)=(Total Sum of the diameter from above 5 reading)/5
Radius of the wire(r)=d/2
Length of the wire=l
Please make sure all the observation are in same units
Specific Resistance of the wire=(3.14)r2X/l
[iframe width=”560″ height=”315″ src=”https://www.youtube.com/embed/OWIpKd3FWUU” frameborder=”0″ allowfullscreen][/iframe]
Viva Voice question for Meter Bridge/Wheat Stone Bridge
Q1 what do you mean by a resistance?
Ans: when a potential difference is applied across a conductor, the free electrons start moving in particular directions. While moving through the materials these electrons collide with other atoms and molecules .they oppose this flow of electrons through it, this opposition is called resistance
Q2 Explain the law of resistance? or How does the resistance of a wire depend on its dimensions?
Ans: The resistance of a wire depends upon the various factors:
1. It directly proportional to its length L.
2. It is inversely proportional to its area of cross section A.
3. It depends upon the nature of the material.
4. It also depends upon the temperature of the wire.
Q3 Answer these
a) What is the range of Low resistance
Ans:Low Resistance: order of 1 ohm and under
b) What is the range of Medium resistance
Ans:Medium Resistance: 1 ohm upwards to about 0.1 M Ohm
resistances.
c)What is the range of High resistanceHigh Resistance: All resistances of the order of 0.1 MOhm and upwards
Q4. Explain Wheatstone bridge?
Ans: The Wheatstone bridge is an instrument for making comparison measurements and operates upon a null indication principal.All details are explained above
Q5. What are the factors affects the measurements of medium resistance?
Ans: The following factors affect the measurements of medium resistance:
1. Resistance of contact leads
2. Thermoelectric effects
3. Temperature effect
4. Contact resistance
5. Change in ratio arms
6. using a high resistance
Q6. What are the limitations of Wheatstone bridge?
Ans: The use of Wheatstone bridge is limited to the measurement of resistances ranging from a few Ohm to several Mega Ohm. The upper limit is set by the reduction in sensitivity to unbalance caused by high resistance values.
Q7. What are the methods used to measure high resistances?
Ans: The different methods employed for measurement of high resistance are:
1. Direct deflection method
2. Loss of charge method
3. MegaOhm method
4. Megger
Q8: In a given meter bridge set up, the null point is obtained at a length l cm. If without making any other change, the radius of the meter bridge is doubled, what would be the likely position of the null point now?
Answer Same
Q9:What happens to the resistivity of a wire when it is double folded?
Q10: Why do we use thick copper strips to connect the wire of the meter bridge to the rest of the set up?
Q11:Name the SI unit of the specific resistance (resistivity).
Q12:Why constantan or manganin wires are used for making the resistance coils in resistance box?
Q13.Why is ammeter always connected in series and voltmeter always connected in parallel?
Q14 what are the different methods used for measurement of medium resistances?
Ans: the different methods used for measurement of medium resistances are:
1. Ammeter- voltmeter method
2. Substitution method
3. Wheatstone bridge method
4. Ohmmeter method
Q15 what are the different methods used for measurement of Low resistances?
Ans: the different methods used for measurement of medium resistances are:
1. Potentiometer
2. Ammeter- voltmeter method
3. Kelvin double Bridge method
Q16: Why does galvanometer show opposite deflection in meter bridge experiment?
Answer:In meter bridge experiment we are using a center zero galvanometer.
The galvanometer has two terminals; we shall call one terminal as X and the other as Y
If VX > VY , then a current will flow from X to Y through the galvanometer and makes the needle to move from its center zero position. Let us say it moves to the right.
If VX < VY, then the current will be reversed and the needle moves to the left from its zero position.
If VX = VY i.e., if the potential difference is zero, no current flows through the galvanometer and the needle remains in its zero position.
By adjusting the jockey, we find the position where there is no potential difference between the two terminals of the galvanometer.
Must Read Articles
Screw Gauge physics experiment
Vernier caliper(physics practicals for class 11)
Frequently used basic physics equations

What happens if we interchange the components in left and right gap of meter bridge?
Hi, As you can see from the whetstone bridge we have resistances in all the four arms. Now in the meter bridge if you interchange the components of left and right gaps which are both resistances the circuit should work fine because you are interchanging one resistor with other. Now you have one known and one unknown resistance if left one has unknown resistance now then you might have to look at your formula for calculating unknown as now you have known resistance on right.
when a metal conductor connected to left gap of a matre bridge is heated,the balancing point is