
Horizontal range of projectile formula derivation
I have written lots of words to explain how to do the derivation but you do not have to write this much when doing this derivation in exams. Simply write whatever is necessary to prove the point.
When a projectile is launched it takes a parabolic path and the range of this parabola is given by the relation
\[R=\frac{{v_0}^2}{g}\times \sin2\theta_0 \tag{1}\]
But the question is how did we get this relation for the range of the projectile.
To derive this formula let us consider the figure given below which depicts a ball launched with initial velocity \(v_0\) that makes an angle \(\theta_0\) with the horizontal. This ball then travels in a parabola and we have to work out the range formula from this given information.
We will now break the process of our derivation into three steps for the sake of ease of learning. The summary of these steps is given below in the form of a concept map.
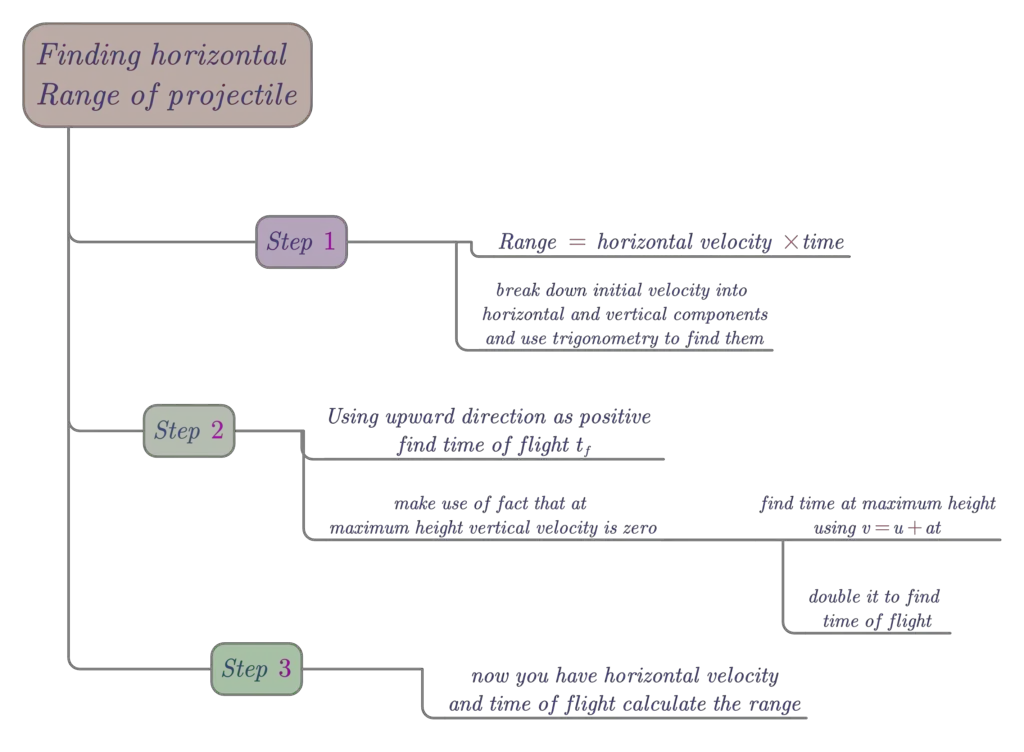
We know that
\(distance= speed \times time\)
So, we need two things to get the formula for horizontal range
- horizontal speed
- time is taken by projectile to reach the final position from the initial position.
Step 1:
Now we are given initial velocity with which projectile is launched. We will first break down initial velocity into two components (since velocity is a vector quantity) as shown below in the figure.
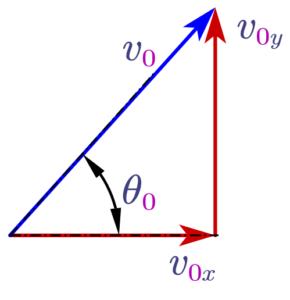
(a) Horizontal component \(v_{0x}\)
(b) Vertical component \(v_{0y}\)
Now from trigonometry horizontal component would be
\[v_{0x}=v_0\cos \theta_0 \tag{2}\]
and vertical component would be,
\[v_{0y}=v_0\sin \theta_0 \tag{3}\]
Equation (2) gives us the horizontal speed now we have to find the time of flight.
Step 2:
If we take upward direction as positive than horizontal range could be given by
\(\text{range}=\text{horizontal speed}\times \text{time}\)
Now we already have knowledge about horizontal speed. In this step, our task is to find the time which projectile has used to reach from the initial position to the final position.
We can use a vertical component of speed to gain knowledge about time. We can find the time that the projectile would take to get to the top (or reach maximum height) and then return to the bottom.
So, the initial vertical velocity is
\(v_{0y}=v_0 \sin\theta_0\)
Let \(t_m\) is the time taken by the projectile to reach the maximum height at highest point vertical component of velocity would be zero that is,
\(v_{0y}=0\)
This can be visualized by drawing a tangent at a point of the maximum height of the parabolic path as shown below in the figure. The direction of this tangent gives the direction of instantaneous velocity at that point. Now if you resolve the vector \(\vec{v}\) it shows that the vertical component of velocity is zero at this point.
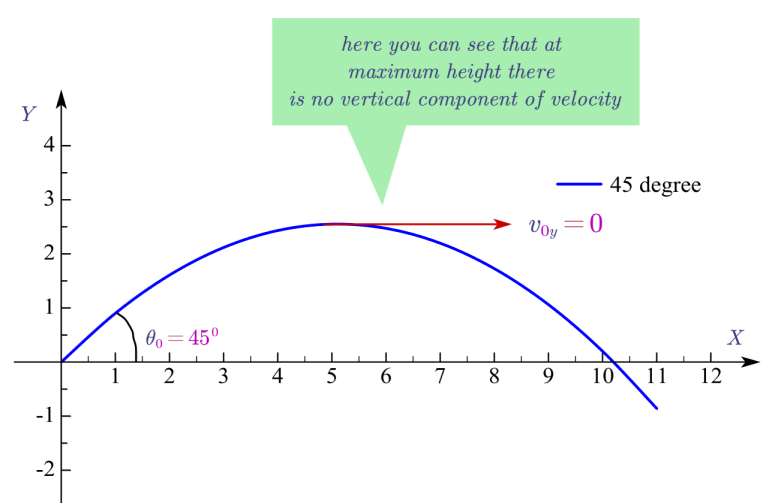
from the first equation of uniformly accelerated motion (See Kinematic equations for uniformly accelerated Motion)
\[v=u+at \tag{4}\]
Here, in this case,
\(v_{0x}=0\)
Initial velocity in the vertical direction
\(v_{0y}=v_0\sin\theta_0\)
Acceleration due to gravity is
\(a=-g\)
because we are taking upward direction as positive.
Substituting all these values in equation (4) we get
\[0=v_0\sin\theta_0-gt_m\]
or,
\[t_m=\frac{v_0\sin\theta_0}{g}\]
We now have time taken by the projectile to reach the maximum height.
From symmetry time taken to reach the bottom would be the same as the time taken to reach the maximum height.
So the total time of flight would be
\[t_f=2t_m\]
or,
\[t_f=\frac{2v_0\sin\theta_0}{g}\]
Step 3:
Now, we have total time taken by projectile to reach from initial position to final position we also have an initial velocity of projectile along horizontal direction so the
\(range= \text{horizontal speed} \times \text{time of flight}\)
\[Range=v_0\cos\theta_0 \times \frac{2v_0\sin\theta_0}{g} = \frac{{v_0}^2(2\sin\theta_0\cos\theta_0)}{g}\]
From trigonometry identity, we know that
\(2\sin\theta\cos\theta=\sin2\theta\)
This is our final result is
\[Range=R=\frac{{v_0}^2}{g}\times \sin2\theta_0\]
