Similarity – Geometry
(basics and concept:- similarity math)
Geometry is a branch of mathematics. While studying geometry we are concerned with questions of shape, size, the relative position of figures, and the properties of space. This article is about similarity (geometry) as we study in math. The figure below shows various figures having the same color are similar figures.
We often come across objects that have different sizes but similar shapes, for example, an Indian one rupee coin and 5 rupee coin have different size but same shape. They both are circular in shape. Refer to the figure given below
Similarity encountered in day to day life. We have also learned about congruency in class 7 maths and class 9 maths. There is a difference between congruent figures and similar figures. When two shapes/figures are congruent they are exactly equal in their shape and size. In the case of similarity math, two shapes (or figures) can be similar if they have the same shape. Similar shapes may have different size. From this statement, we can say that all congruent figures are similar but all similar figures are not congruent.
Similarity math definition:- The similarity is denoted by the symbol \(\sim\) . Two figures having the same shape (and not necessarily the same size) are called similar figures.
Similarity geometry examples
- all circles are similar
- two (or more) squares are similar
- two (or more) equilateral triangles are similar
It can be observed in the case of circles, all squares are similar and all equilateral triangles are similar.
Note that all congruent figures are similar but the similar figures need not be congruent.
Similarity statement geometry (similar polygons)
Again let us consider the figure given below where we have two quadrilaterals \(ABCD\) and \(PQRS\)
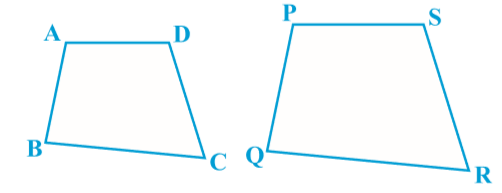
When we first look at them they appear to be similar but we are not 100% sure about it. So, we must have some definition or conditions for the similarity of figures. Based on this definition we can decide whether two figures are similar or not. The essence of the similarity of two figures and in particular of two polygons is
Similarity statement for polygons:-
Two polygons of the same number of sides are similar, if
( i ) their corresponding angles are equal and
(ii ) their corresponding sides are in the same ratio (or proportion).
Above similarity statement for polygons must hold true for similar polygons.
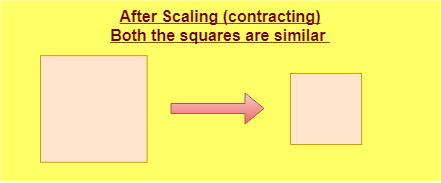
Two or more geometrical objects are similar if they have the same shape or one is the mirror image of the other. Similar images or shapes can also be obtained by uniformly scaling (enlarging or contracting) the image in question. The figure given below shows two squares where the second square (on right) is obtained after contracting the first square (left square)
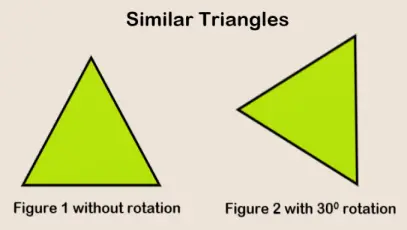
Translation, reflection or rotation of an image along with (or without) its scaling results in an image similar to the original one. The figure below shows two similar figures which result due to the rotation.
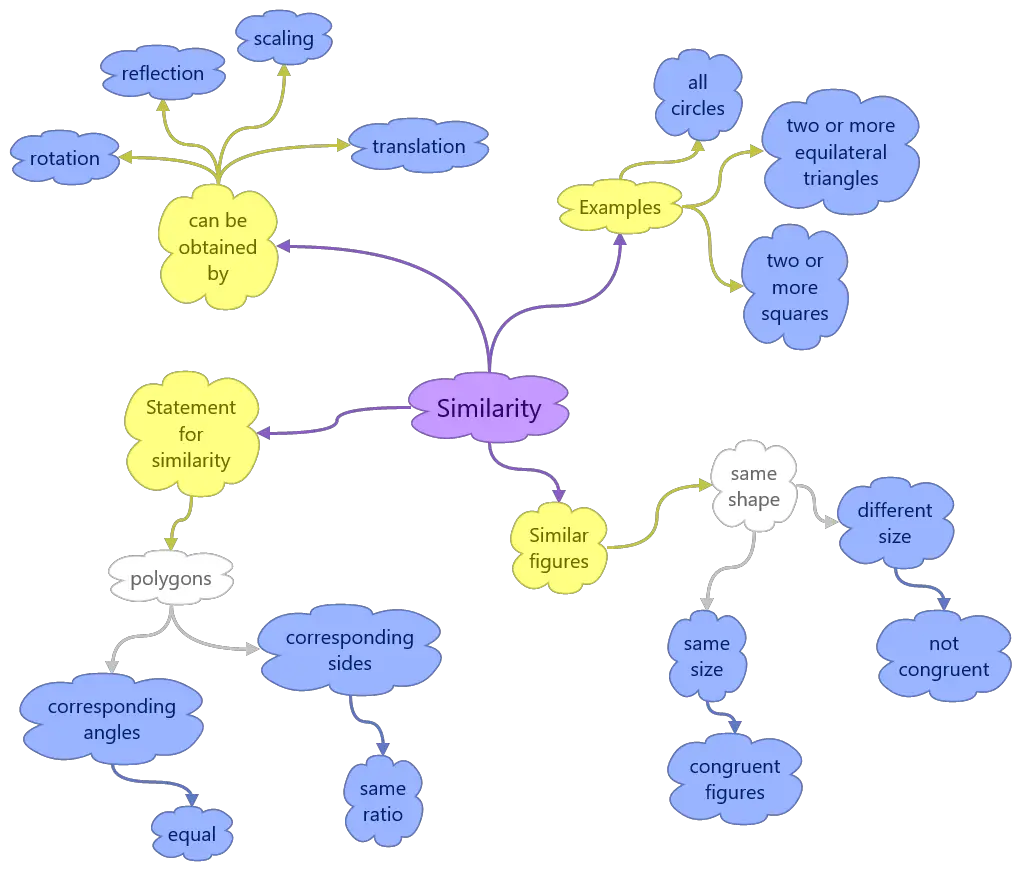
Similarity math (geometry) mind/concept map
The figure below shows an easy to memorize mind map for similarity in math (geometry). Pdf download of this mind map is also available.
Download this concept map as pdf
Follow this link about similar triangles to know more.
You can check also ncert solutions for class 10 maths for practice