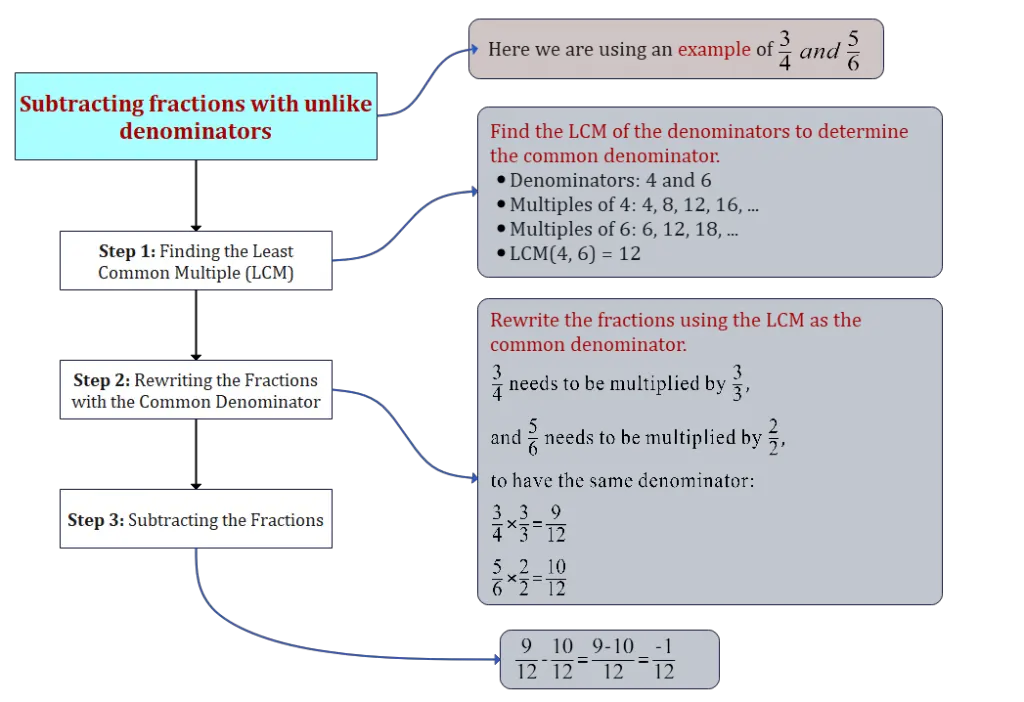
In this article, we will learn about subtracting fractions with unlike denominators. If you do not know what are fractions with unlike denominators consider reading this article
Subtracting fractions with unlike denominators
Definitions and Concepts
Fraction
- A fraction represents a part of a whole and consists of a numerator and a denominator. For example, \(\frac{a}{b}\), where \(a\) is the numerator and \(b\) is the denominator.
Unlike Denominators
- Two fractions have unlike denominators if the denominators are not the same.
Subtracting Fractions with Unlike Denominators
Step 1: Finding the Least Common Multiple (LCM)
To subtract fractions with unlike denominators, find the least common multiple of the denominators.
Example:
LCM of 4 and 6:
\[
\text{LCM}(4, 6) = 12
\]
Step 2: Rewriting the Fractions with the Common Denominator
Next, rewrite both fractions using the LCM as the common denominator.
Example:
Rewrite \(\frac{3}{4}\) and \(\frac{5}{6}\) with 12 as the common denominator.
\[
\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}
\]
\[
\frac{5}{6} = \frac{5 \times 2}{6 \times 2} = \frac{10}{12}
\]
Step 3: Subtracting the Fractions
Subtract the numerators and place the result over the common denominator.
\[
\frac{9}{12} – \frac{10}{12} = \frac{9 – 10}{12} = \frac{-1}{12}
\]
Solved Examples
let us have a look at two examples of subtracting fractions with unlike denominators.
Example 1: Subtracting \(\frac{2}{7}\) from \(\frac{3}{5}\)
Step 1: Finding the Least Common Multiple (LCM)
Find the LCM of 7 and 5:
\[
\text{LCM}(7, 5) = 35
\]
Step 2: Rewriting the Fractions with the Common Denominator
\[
\frac{2}{7} = \frac{2 \times 5}{7 \times 5} = \frac{10}{35}
\]
\[
\frac{3}{5} = \frac{3 \times 7}{5 \times 7} = \frac{21}{35}
\]
Step 3: Subtracting the Fractions
\[
\frac{3}{5} – \frac{2}{7} = \frac{21}{35} – \frac{10}{35} = \frac{11}{35}
\]
Example 2: Subtracting \(\frac{7}{8}\) from \(\frac{3}{5}\)
Step 1: Finding the Least Common Multiple (LCM)
\[
\text{LCM}(8, 5) = 40
\]
Step 2: Rewriting the Fractions with the Common Denominator
\[
\frac{7}{8} = \frac{35}{40}
\]
\[
\frac{3}{5} = \frac{24}{40}
\]
Step 3: Subtracting the Fractions
\[
\frac{3}{5} – \frac{7}{8} = \frac{-11}{40}
\]
These two examples shows the methodical approach of subtracting fractions with unlike denominators. By finding the LCM, rewriting the fractions, and performing the subtraction, we can obtain the desired results.
Questions and Answers
1. Subtract \(\frac{2}{3}\) from \(\frac{5}{6}\):
\[
\frac{5}{6} – \frac{2}{3} = \frac{5}{6} – \frac{4}{6} = \frac{1}{6}
\]
2. What if the fractions are mixed numbers?
Convert them into improper fractions and then follow the steps above.
Further Reading
If you are interested in building a strong foundation in mathematics, particularly focusing on basics suitable for younger grades, we invite you to explore our resources tailored for students. Visit Class 6 Maths for fundamental concepts, and Class 7 Math to continue your learning journey.