Trigonometry formulas for class 10

Students can get trigonometry formulas for Class 10 here. Trigonometry is the study of the relationships between triangle angles, lengths, and heights. It contains ratios, functions, identities, and formulas for solving issues based on right-angled triangles. Trigonometry is also used in engineering, astronomy, physics, and architectural design. This chapter is crucial since it covers a wide range of topics such as linear algebra, calculus, and statistics.

In CBSE Class 10, trigonometry is introduced. It is a completely new and difficult chapter in which one must memorize all of the formulas and apply them correctly. The formulas for Trigonometry Class 10 are listed here.

Trigonometry formulas List for class 10

Trigonometry is quite an important chapter in Class 10 maths and a lot of good questions come in board examination also. Here are the trigonometry formulas for class 10 on one page

In a right angle triangle ABC where B=90°

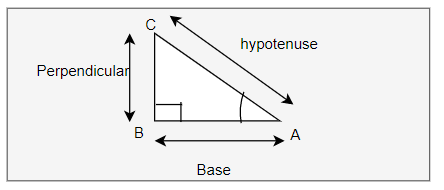
We can define the following term for angle A

Base:  Side adjacent to the angle

Perpendicular: Side Opposite of angle

Hypotenuse: Side opposite to right angle

We can define the trigonometric ratios for angle A as

$\sin A=  \frac {Perpendicular}{Hypotenuse} =\frac {BC}{AC}$

$cosec A= \frac {Hypotenuse}{Perpendicular} =\frac {AC}{BC}$

$\cos A= \frac {Base}{Hypotenuse} =\frac {AB}{AC}$

$sec A= \frac {Hypotenuse}{Base}=\frac {AC}{AB}$

$\tan A= \frac {Perpendicular}{Base} =\frac {BC}{AB}$

$\cot A= \frac {Base}{Perpendicular}=\frac {AB}{BC}$

Notice that each ratio in the right-hand column is the inverse, or the reciprocal, of the ratio in the left-hand column.

Reciprocal of functions

$cosec A = \frac {1}{\sin A}$

$ \sec A = \frac {1}{\cos A}$

$\cot A =\frac {\cos A }{\sin A} = \frac {1}{\tan A}$

Trigonometric ratio from complementary angle in Right angle triangle

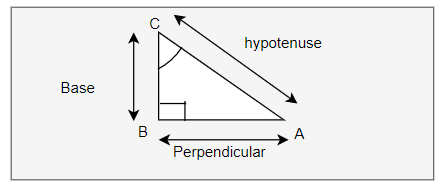
$\sin C= \frac {Perpendicular}{Hypotenuse} =\frac {AB}{AC}$

$cosec C= \frac {Hypotenuse}{Perpendicular} =\frac {AC}{AB}$

$\cos C= \frac {Base}{Hypotenuse} =\frac {BC}{AC}$

$\sec C= \frac {Hypotenuse}{Base}=\frac {AC}{BC}$

$\tan A= \frac {Perpendicular}{Base} =\frac {AB}{BC}$

$\cot A= \frac {Base}{Perpendicular}=\frac {BC}{AB}$

This can also be written as C= 90 -A

$\sin (90-A) =\cos(A)$

$\cos(90-A) = \sin A$

$\tan(90-A) =\cot A$

$\sec(90-A)= cosec A$

$cosec (90-A) =\sec A$

$\cot(90- A) =\tan A$

Trigonometric identities

$\sin^2 A + \cos^2 A =1$
$1 + \tan^2 A =\sec^2 A$
$1 + \cot^2 A =cosec^2 A$

Trigonometric Ratios of standard angles

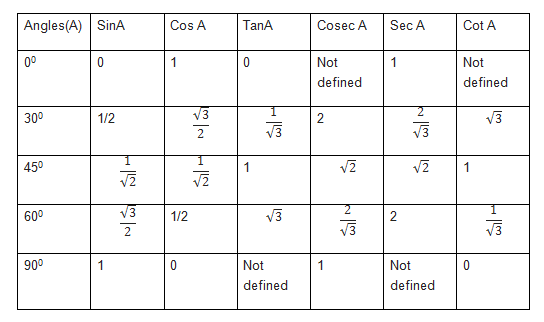
You can below post on how to remember this easily

How to easily remember trigonometric ratios table

How to Find trigonometric ratios in case one is given

$ \sin A = \sqrt {1 – \cos^2A}$

$ \cos A = \sqrt {1 – \sin^2A}$

$ \tan A = \frac {\sin A}{\sqrt {1 – \sin^2A}} = \frac {1}{\cot A} = \sqrt { \sec^2 A -1}  = \frac {1}{\sqrt { cosec^2 A -1} }$

$ \cot A = \frac {1}{\tan A}$

$\sec A = \sqrt { 1 + \tan^2 A} = \frac {1}{\cos A}$

$cosec A = \sqrt {1 + \cot^2 A} = \frac {1}{\sin A}$

Range of Values of trigonometric ratios

Values of Sin A and cos A is always less than or equal to 1

Values of sec A and cosec A is always greater than or equal to 1

Double Angle Formula

$\sin 2A = 2 \sin A \cos A$
$\cos 2A= \cos^2 A – \sin^2 A =2\cos ^2 A – 1= 1 – 2 \sin^2 A= \frac { 1 – \tan^2 A}{1+ \tan^2 A}$
$\tan 2A= \frac { 2\tan A}{1 -\tan^2 A}$

Triple Angle Formula

$\sin 3A = 3 \sin A – 4 \sin ^3 A$
$\cos 3A = 4 \cos^3 A – 3 \cos A$
$\tan 3A= \frac { 3 \tan A – \tan^3 A}{1 – 3\tan^2 A}$

Solved Questions

Question 1

Find the value of sin A, cos A, and tan A in the triangle having opposite side = 3 cm, adjacent side = 4 cm, hypotenuse = 5 cm.

Solution

• \(\sin A = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{3}{5} = 0.6\)
• \(\cos A = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{4}{5} = 0.8 \)
• \(\tan A = \frac{\text{opposite}}{\text{adjacent}} = \frac{3}{4} = 0.75\)

Question 2

Find the value of the following expression: \[\sin 60^\circ \cdot \cos 30^\circ + \cos 60^\circ \cdot \sin 30^\circ \]

Solution

\(\sin 60^\circ = \frac{\sqrt{3}}{2}), (\cos 30^\circ = \frac{\sqrt{3}}{2} \)

\(\cos 60^\circ = \frac{1}{2} \), \(\sin 30^\circ = \frac{1}{2} \)

\[\sin 60^\circ \cdot \cos 30^\circ + \cos 60^\circ \cdot \sin 30^\circ = \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{3}}{2} + \frac{1}{2} \cdot \frac{1}{2} \]
\[= \frac{3}{4} + \frac{1}{4} = 1\]

Question 3

A ladder 10 m long leans against a vertical wall, making an angle of 60° with the ground. Find the height at which the ladder touches the wall.

Solution

Given: ladder length = 10 m, angle with ground = 60°.

Height \(h = 10 \sin 60^\circ = 10 \cdot \frac{\sqrt{3}}{2} = 5\sqrt{3} \) m.

Hope you like this post on trigonometry formulas for class 10 Maths