Acceleration Formula
Acceleration is the rate of change of velocity with time. It is a measure of the change in the velocity of an object per unit time and mathematically acceleration formula is given as
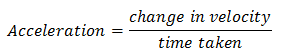
For describing average acceleration, we first consider the motion of an object along a straight line.
Suppose at time t1 object is at point P moving with velocity v1 and at time t2 it is at point Q and has velocity v2. Now average acceleration of an object in moving from P to Q is
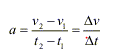
which is the change in velocity of the object with the passage of time.
If the velocity of an object changes from an initial value u to the final value v in time t, the acceleration a is given by,
a=(v-u)/t
and this kind of motion is called accelerated motion.
Important Points about Acceleration Formula
1) Since the velocity of a moving object has both magnitude and direction likewise acceleration depending on velocity has both magnitude and direction and hence acceleration is a vector quantity.
2) SI unit of acceleration is ms-2
3) A body has uniform acceleration if it travels in a straight line and its velocity increases by an equal amount in equal intervals of time for example freely falling bodies, the motion of the ball rolling down the inclined plane etc.
4) A body has non-uniform acceleration if its velocity increases or decreases by the unequal amount in equal intervals of time.
5) If acceleration is in the direction of the velocity then it is positive acceleration and if it is in the direction opposite to the direction of velocity then it is negative and the negative acceleration is termed retardation or deceleration.
A motorbike moves in a straight road. The velocity at point A is 36 km/hr, It presses the accelerator paddle and reaches point B in 10 sec. The velocity at point B is 54Km/hr
Find the average acceleration of the car from point A to point B?
Average acceleration is given by
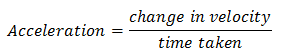Initial velocity= 36 km/hr=10 m/sFinal Velocity = 54 km/hr=15 m/s
Average acceleration= (15-10)/10= .5 m/s2
True and False Statement
a) Acceleration is a scalar quantity?
b) if the velocity of the object is zero, then acceleration will always be zero
c) If a car is moving fast, does it always have acceleration?
Solution
a) False. Acceleration is vector quantity
b) False.
c) False. Fast does not mean acceleration always. It may be moving with high velocity but velocity may not be changing
Motion with constant acceleration
Motion with constant acceleration or uniformly accelerated motion is that in which velocity changes at the same rate throughout the motion.
Here are the equations for uniformly accelerated motion in a straight line
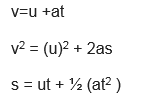
Where
v=Final Velocity
u=Initial Velocity
a= Constant acceleration
t= time interval
s= displacement
A train starts from rest and accelerates uniformly at the rate of 5 m/s2 for 10 sec.
a) Calculate the velocity of the train in 10 sec.
b) Distance traveled by train in 10 sec
Solution
Here it is the example of uniformly accelerated motion
a=5 m/s2
u=0
t=10 sec
v=?
s=?
From
v=u +at
v= 0 + 5×10
=50 m/sec
From
s = ut + ½ (at2 )
s= ½ (5×102 )=250 m
Instantaneous acceleration formula
The acceleration of the moving body at any instant of time is defined as its instantaneous acceleration.
Instantaneous acceleration can be defined in the same way as instantaneous velocity
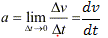
The instantaneous acceleration at any instant is the slope of v-t graph at that instant.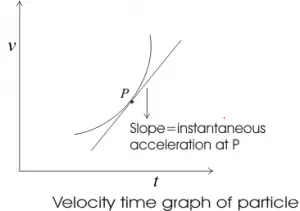
Above figure shows instantaneous acceleration at point P is equal to the slope of the tangent at this point P.
A train is moving on the rail track. The distance traveled by it is defined by the following equation:
x = t3 + t + 4
Find the instantaneous acceleration at time t = 1 sec?
Solution
Now
x = t3 + t + 4
We know that v= dx/dt
So
v= 3t2+1
Acceleration would be given by
a =6t
So, instantaneous acceleration at time t = 1 sec
= 6 m/s2
How to solve problems involving time-dependent acceleration
Here I tried to sum up the steps to solve problems involving time-dependent acceleration. We can easily calculate the position of the particle/object
- Consider that acceleration a is some function of time such that
$a=f(t)$
this equation can also be written in terms of velocity i.e.
$a=\frac{dv}{dt}=f(t)$ …..1 - Now we integrate equation 1 as a function of time
$dv=f(t)dt$
$v=\int dv=\int f(t)dt +C$ ……2
here C is some constant of integration and can be calculated from the initial conditions. - Now we know that $v=\frac{dx}{dt}$ , using this in the solution of equation 2 we can easily find the position of the particle.
Question 1
On a highway with speed limit 80km/h, a car was stopped by applying brakes with a retardation of 5m/s2 in 5 seconds. What is the initial velocity of the car? Was it over-speeding?
Question 2
A cycle traveling with a velocity of 20km/h accelerates at the rate of 0.10m/s2. After what time will it achieve a velocity of 38km/h?
Question 3
A truck moves with a velocity of 36km/h. How much distance will it cover in 1 minute if it moves with a uniform acceleration of 1m/s2?
Question 4
A car starts and attains a velocity of 60m/s in the 30s. If the acceleration is uniform, what is the distance traveled by car to achieve this velocity?
Question 5
A car travelling with a velocity of 10m/s stops on the application of brakes. It produces a uniform retardation of 1.25m/s2. Calculate the distance traveled by car before it comes to rest. Also, find the time taken by the car to stop.
Question 11 What is the acceleration of Honda with a constant velocity of 50 km/h for 20 seconds? Does the car have a constant acceleration?
Question 12 A boy on a bicycle increases his velocity from 5 m/s to 20 m/s in 10 seconds.
a) What is the acceleration of the bicycle?
b) What distance was covered by the bicycle during the 10 seconds?
Acceleration Direction
Acceleration is a vector quantity so it has both magnitude and direction. Direction of acceleration is in the direction of velocity if it is increasing and opposite to the direction of velocity if the velocity is decreasing
Now we use + and – to specify direction in physics. + stands for positive direction and – negative stands for the opposite of positive dimension
if the velocity is in positive direction and it is increasing , acceleration will be positive direction and will be positive
u= 2 m/s ( + as positive direction)
v=3m/s ,t=1 sec
a= (3-2)/1= 1m/s2
o acceleration is positive
if the velocity is in positive direction and it is decreasing, acceleration will be negative direction and will be negative
u= 2 m/s ( + as positive direction)
v=1m/s ,t=1 sec
a= (1-2)/1= -1m/s2
So acceleration is negative
if the velocity is in negative direction and it is increasing , acceleration will be negative direction and will be negative
u= -2 m/s ( – as negative direction)
v=-3m/s ,t=1 sec
a= (-3+2)/1= -1m/s2
So acceleration is negative
if the velocity is in negative direction and it is decreasing , acceleration will be positive direction and will be positive
u= -2 m/s ( – as negative direction)
v=-1m/s ,t=1 sec
a= (-1+2)/1= 1m/s2
So acceleration is positive.
Acceleration in Curvilinear Motion
Centripetal Acceleration Formula
The magnitude of the instantaneous normal acceleration is equal to the square of the speed divided by the radius. Its direction is perpendicular to velocity vector and acts along an inward direction along the radius of the circular path towards the center of the circle.
Because of this, it is called central or centripetal acceleration. The term centripetal means seeking the center.
Centripetal Acceleration Formula = v2/R
Where v is the speed of the object and R is the radius of the circular path
Check out below article to get more information on it
Helpful Related Articles
Acceleration in a curvilinear motion
Circular Motion Physics: Detailed explanation
Hope you like the detailed explanation with examples for acceleration formula. Download of whole article is also given below